Parameter choices

HBT-HERONS has several free parameters that can affect how subhaloes are tracked in time, subject to unbinding, and which thresholds are used to determine if a subhalo is self-bound or not.

The default values that HBT-HERONS uses are intended to provide sensible results, but the inquisitive user may wonder how changing each parameter would affect their results. For this purpose, we provide in this page a series of tests where we highlight how several relevant subhalo-based summary statistics vary when changing the value of these key parameters.

The tests we provide were done using the intermediate resolution ($m_{\mathrm{dm}} = 6.72 \times 10^{9}\,\mathrm{M}_{\odot}$) DMO simulation of the $1\,\mathrm{Gpc}$ box from the FLAMINGO suite of simulations (Schaye et al 2023).

Diagnostic plots

We show how a select number of summary statistics change when varying each free parameter that HBT-HERONS has. The summary statistics were chosen to quantify the instantaneous properties of the subhalo population, as well as their longer term time evolution. Our selection is by no means comprehensive, but it should provide the user the required intuition about how parameters influence the outcome of results.

The statistics are defined as follows:

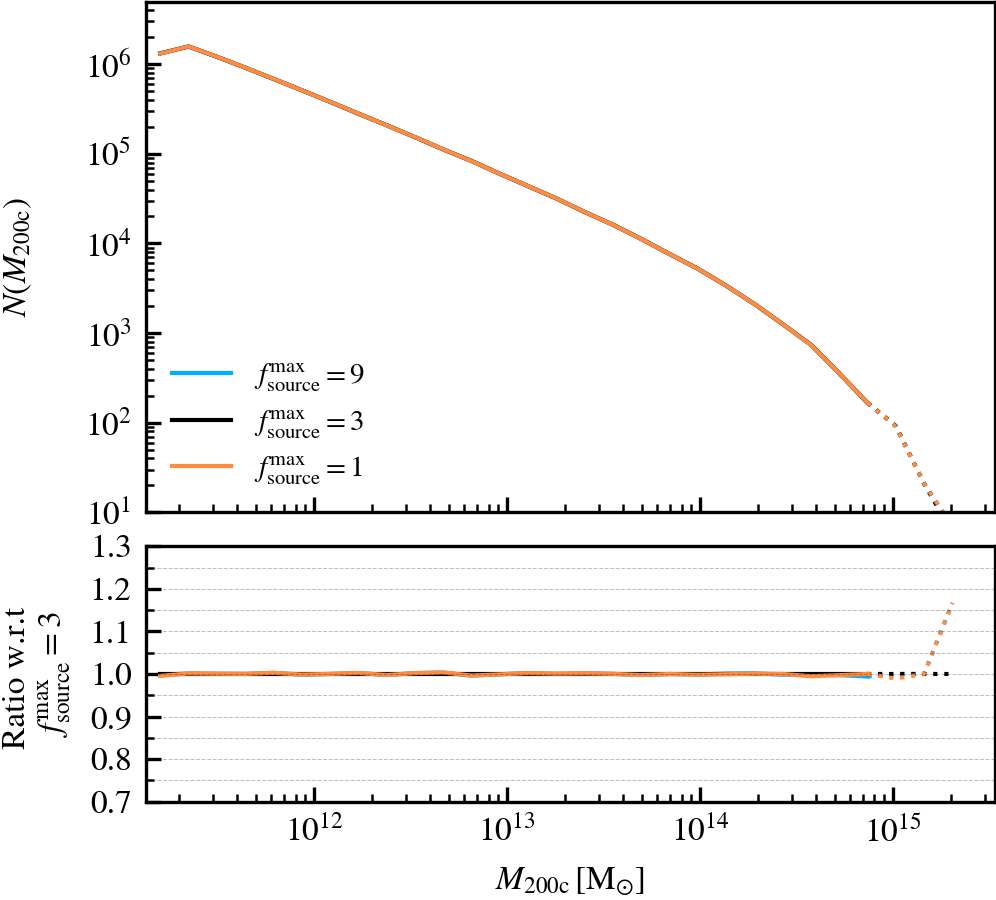
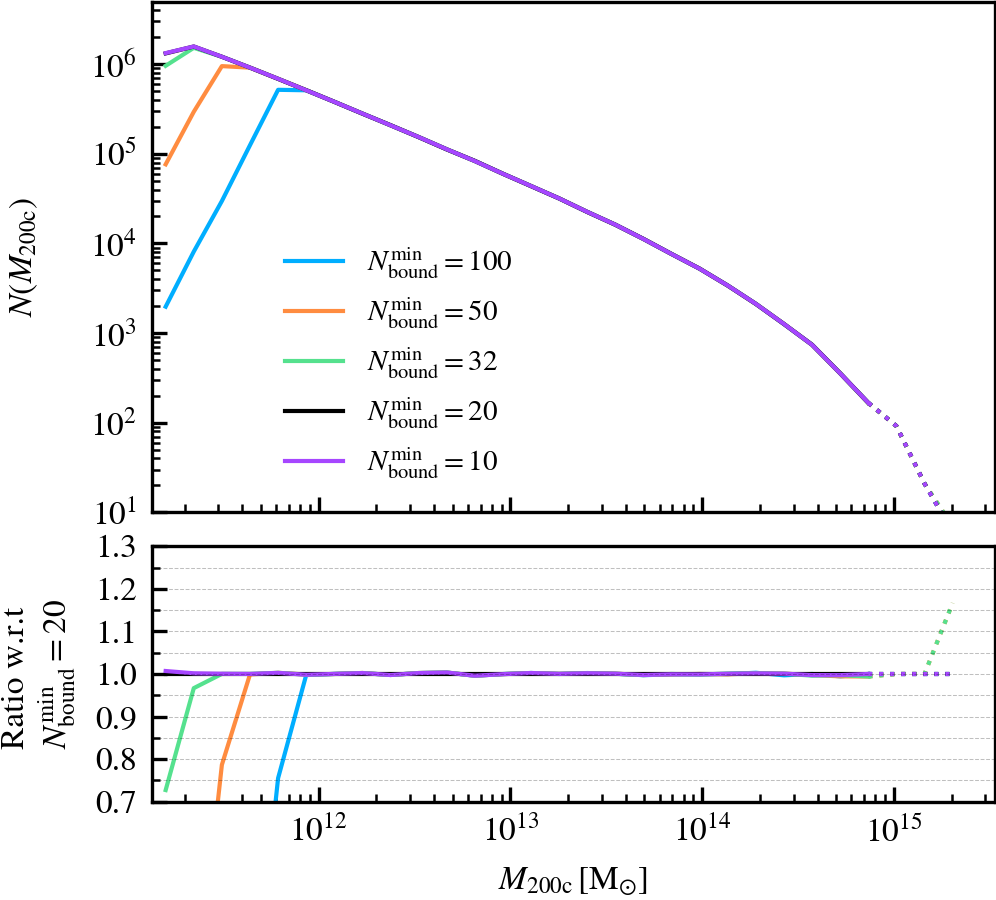
Spherical overdensity mass function ($M_{\mathrm{200c}}$): the number of central subhaloes at $z = 0$, as a function of the mass enclosed by a sphere whose mean enclosed density equals 200 times the critical density of the universe. This definition uses all of the particles enclosed by the sphere, regardless of whether they are bound or not to the central subhalo under consideration.
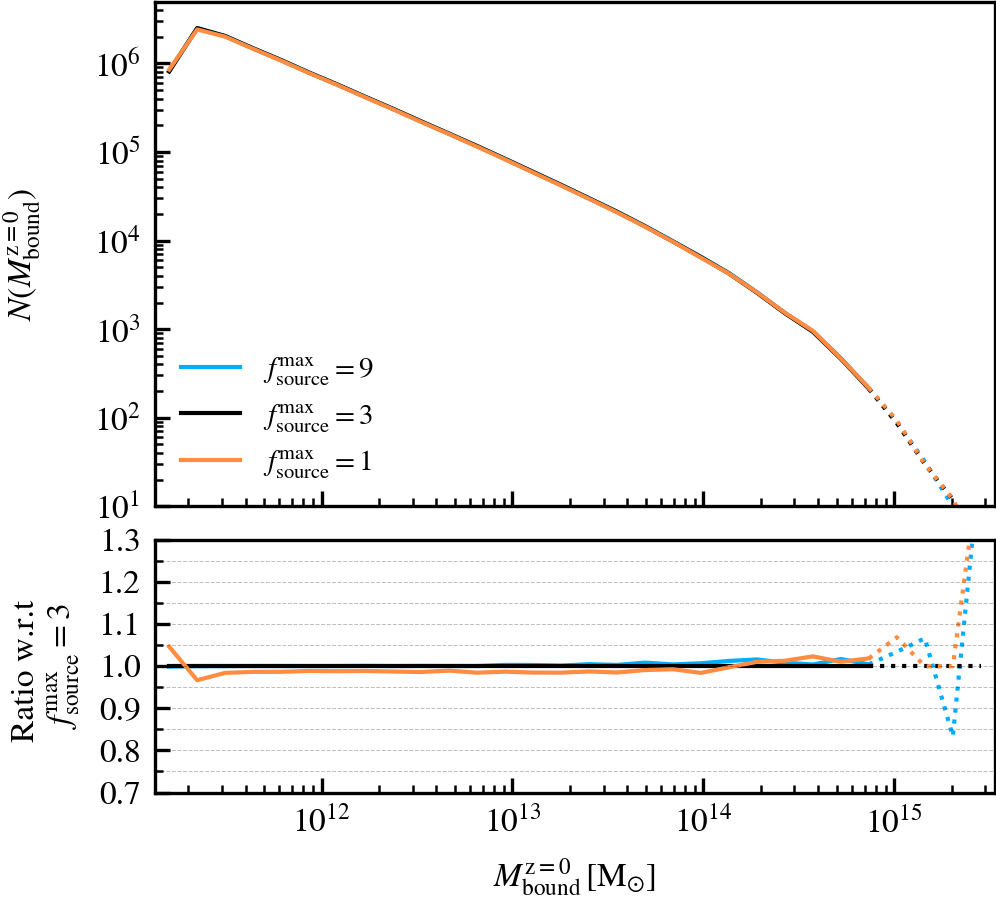
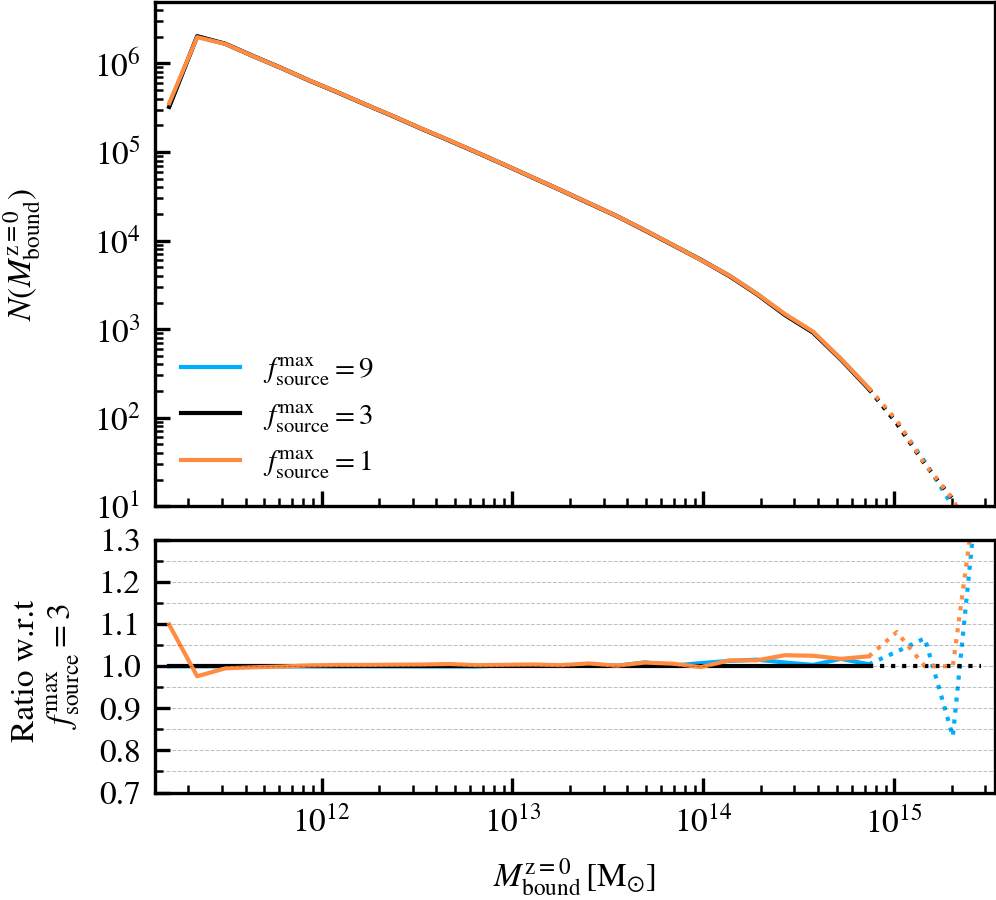
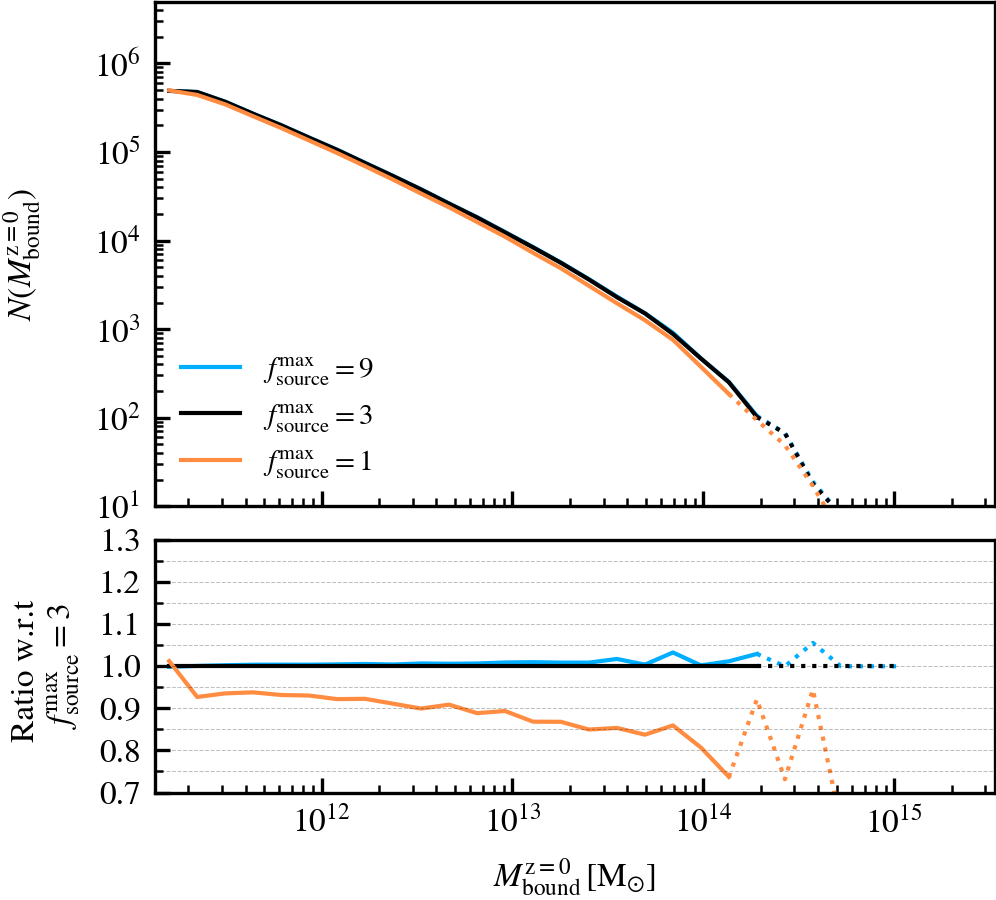
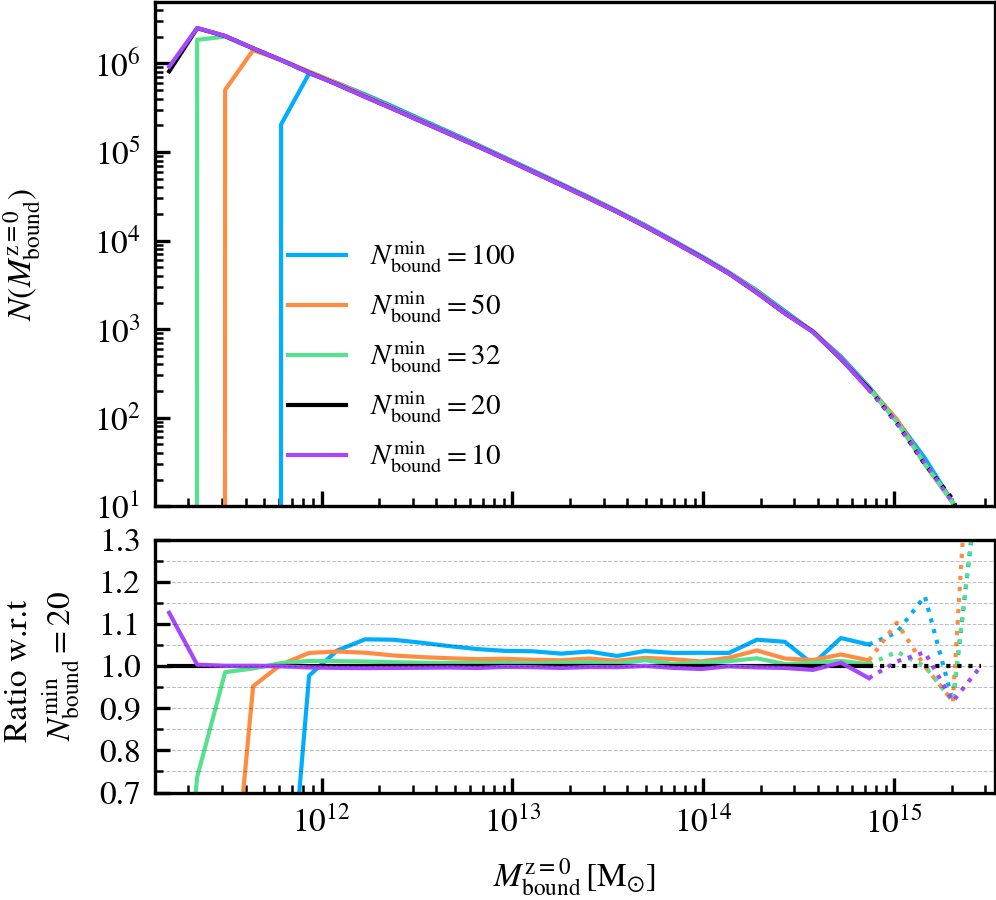
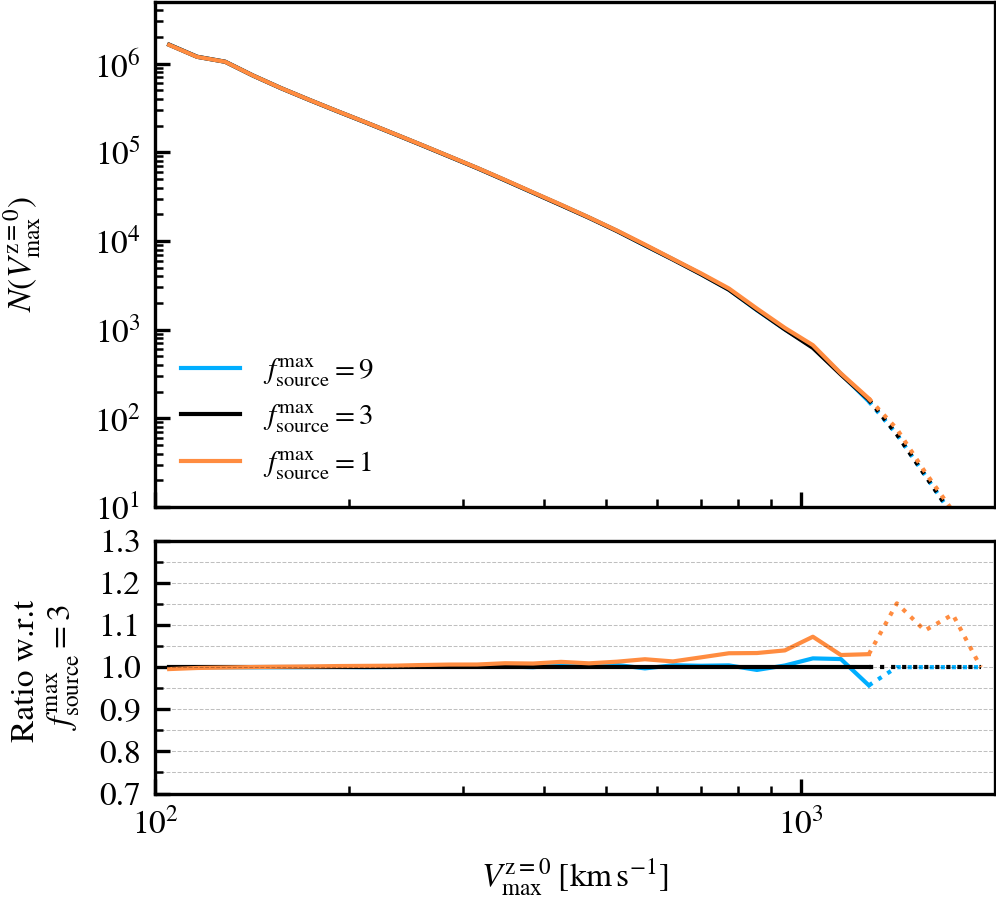
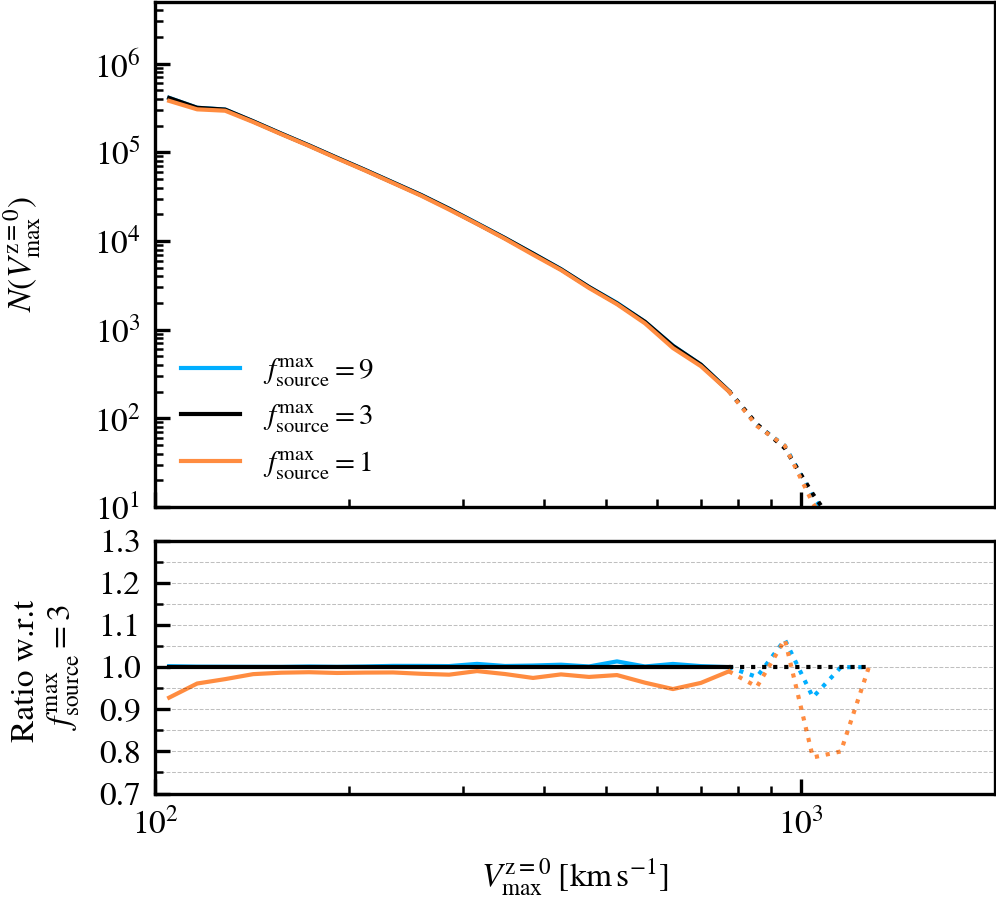
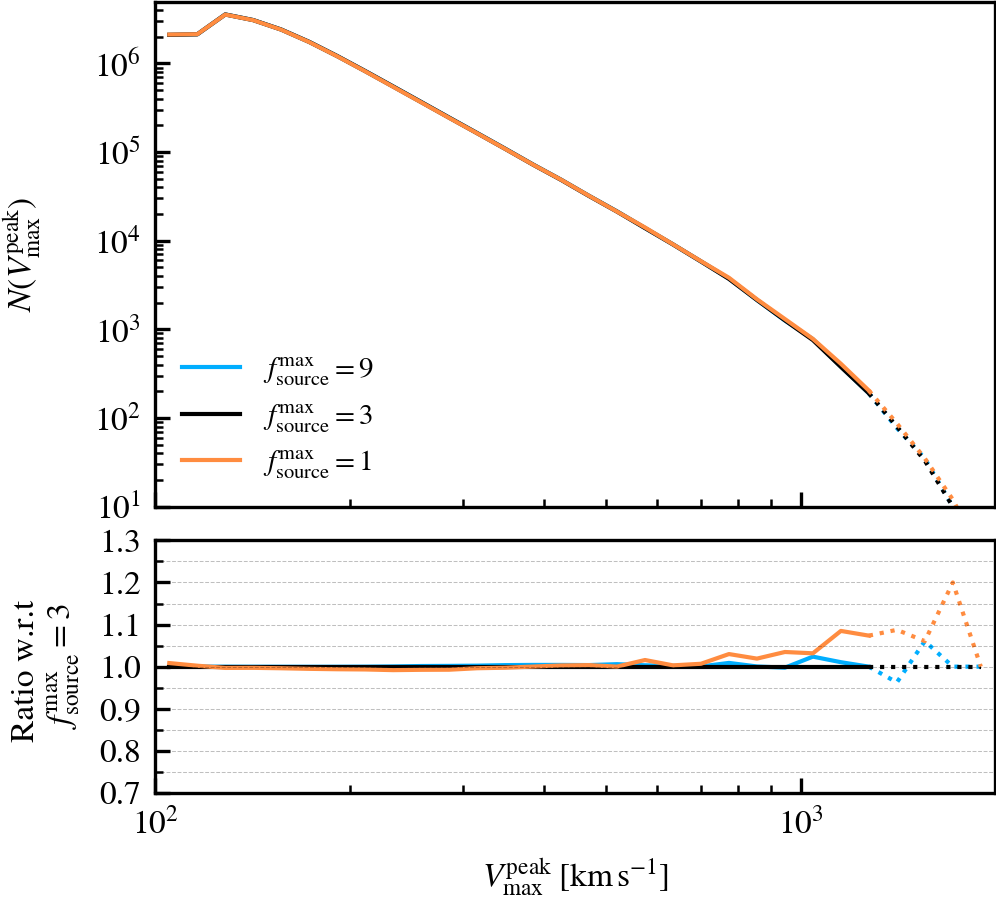
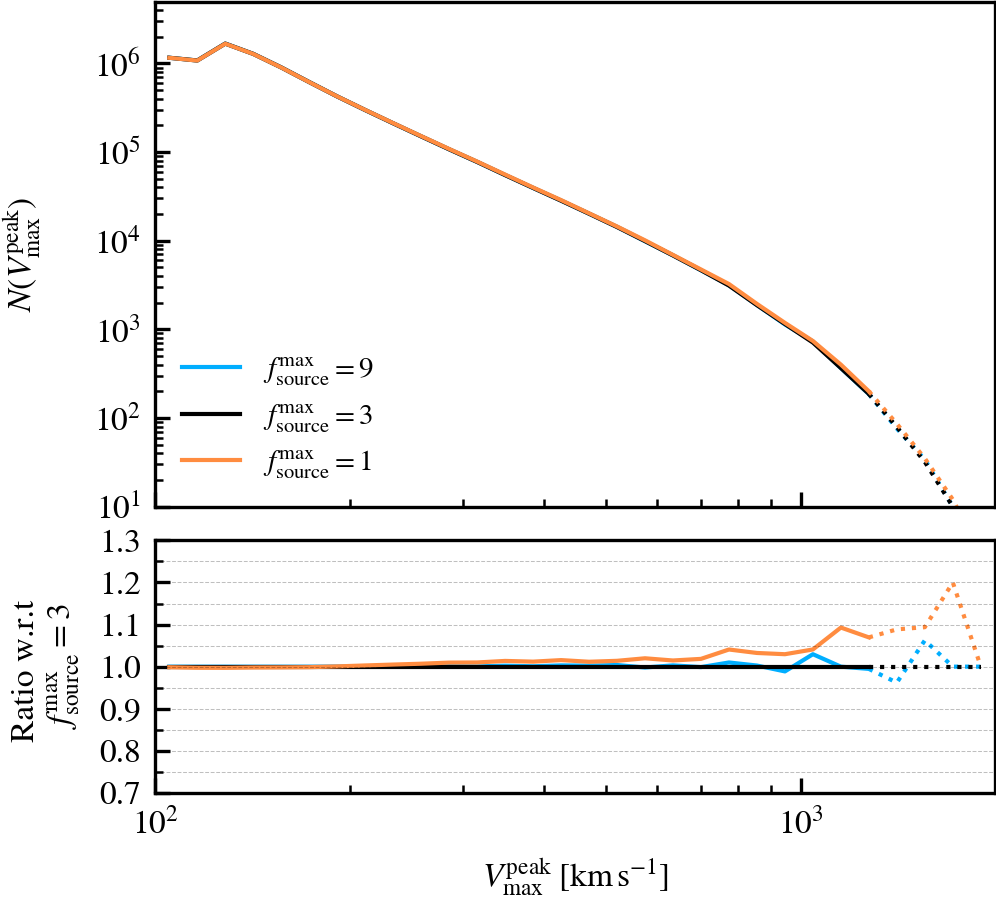
Subhalo mass functions ($M^{i}_{\mathrm{bound}}$): the number of self-bound subhaloes at $z = 0$, as a function of their current bound mass ($M^{\rm z=0}_{\mathrm{bound}}$) or their peak bound mass ($M^{\rm peak}_{\mathrm{bound}}$). The central vs satellite classification is done based on the Depth value of the subhalo at $z = 0$, where Depth = 0 is a central subhalo and a satellite if Depth != 0.
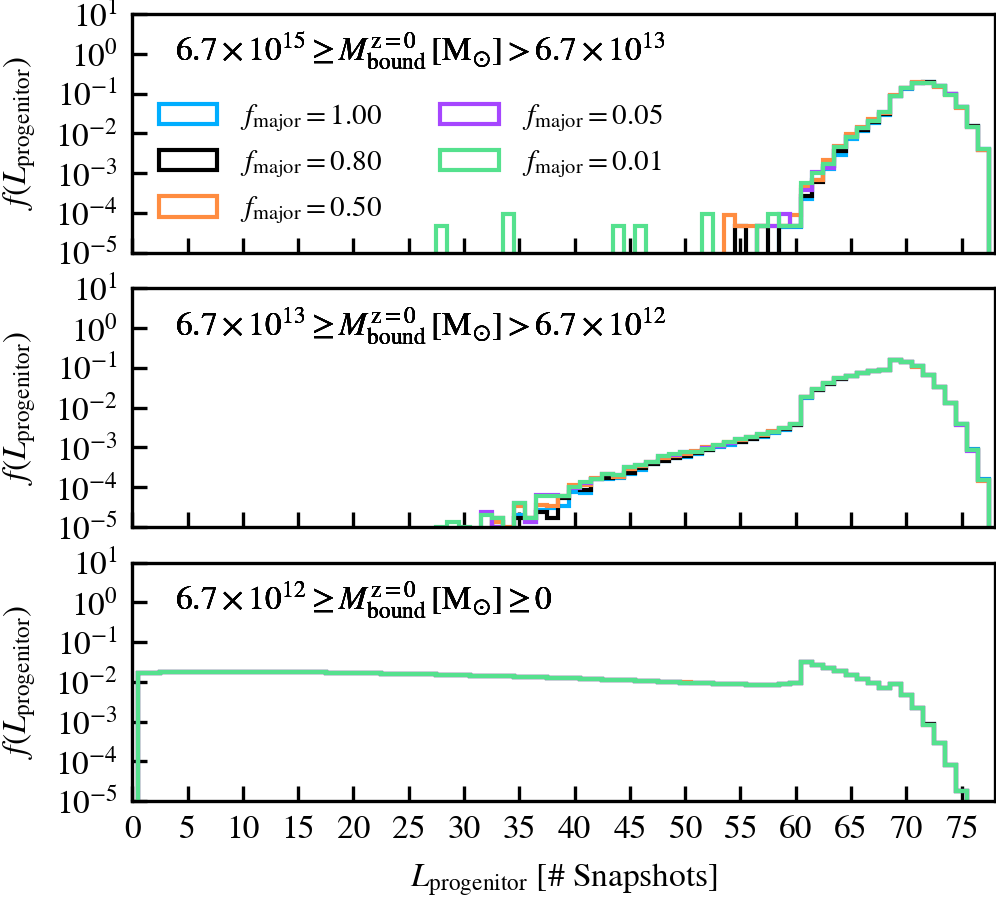
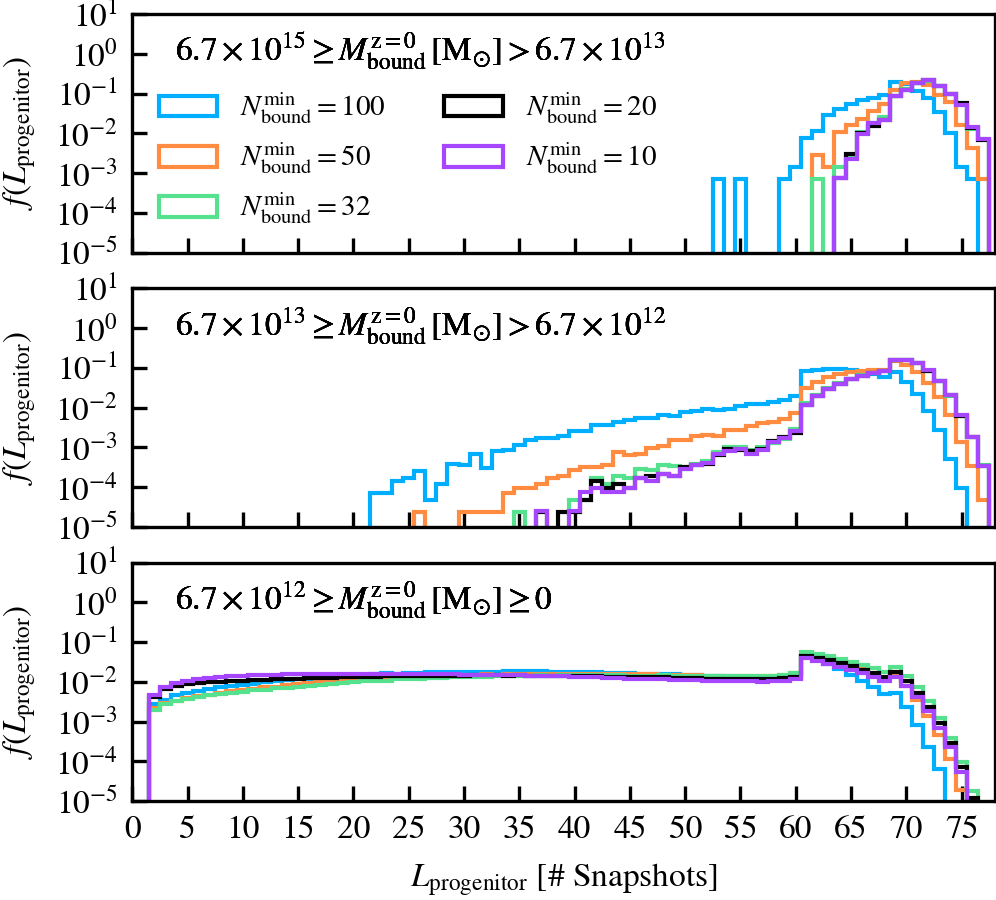
Subhalo velocity functions ($V^{i}_{\mathrm{max}}$): the number of self-bound subhaloes at $z = 0$, as a function of their current maximum circular velocity ($V^{\rm z=0}_{\mathrm{max}}$) or their peak circular velocity ($V^{\rm peak}_{\mathrm{max}}$). The central vs satellite classification is done based on the Depth value of the subhalo at $z = 0$, where Depth = 0 is a central subhalo and a satellite if Depth != 0.
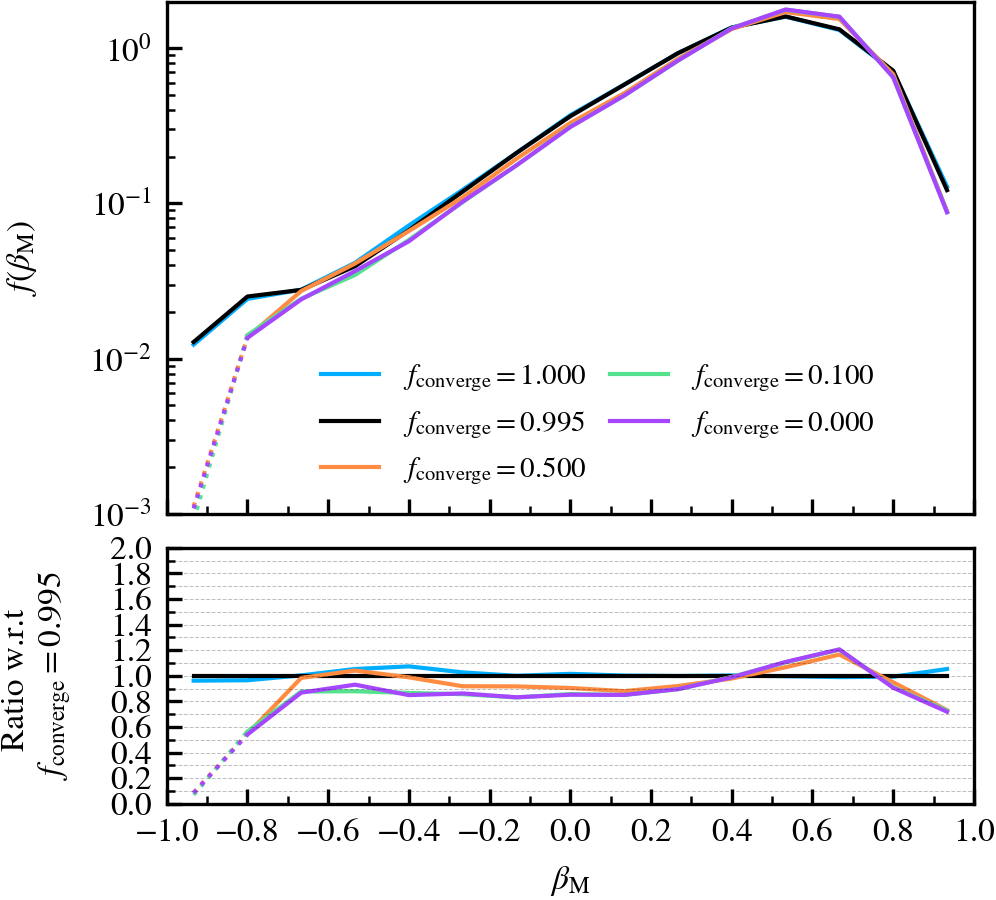
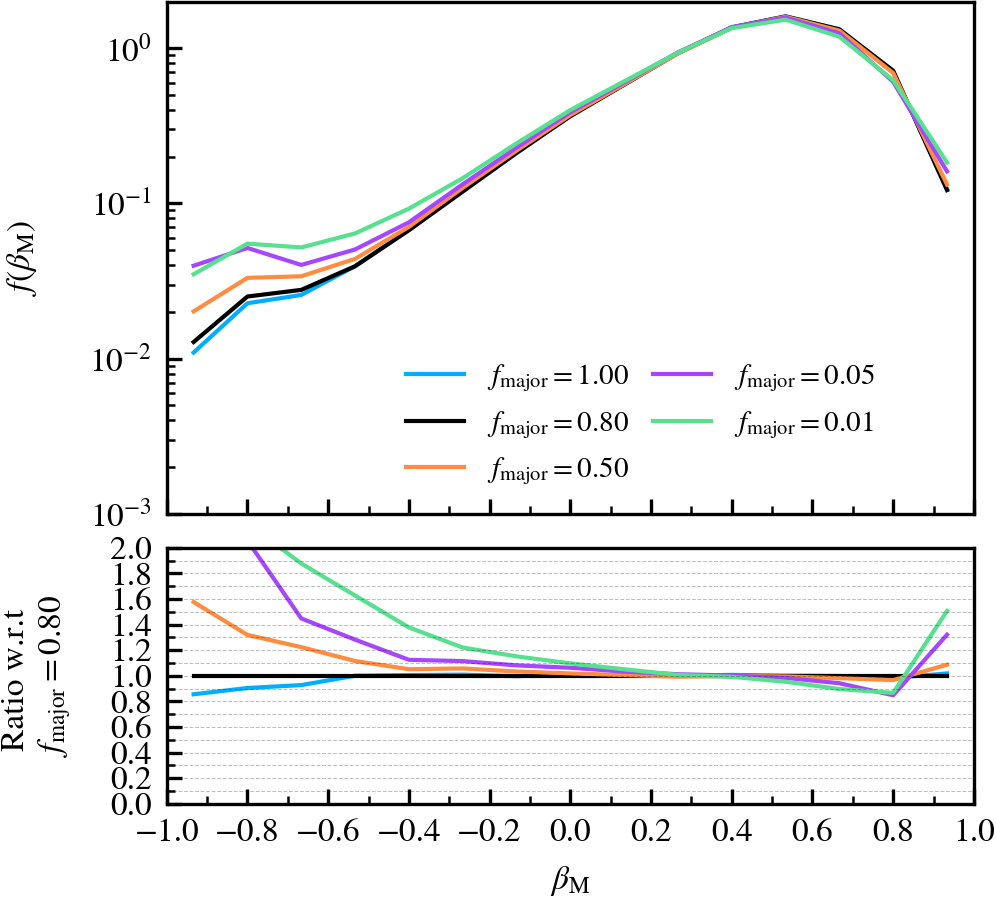
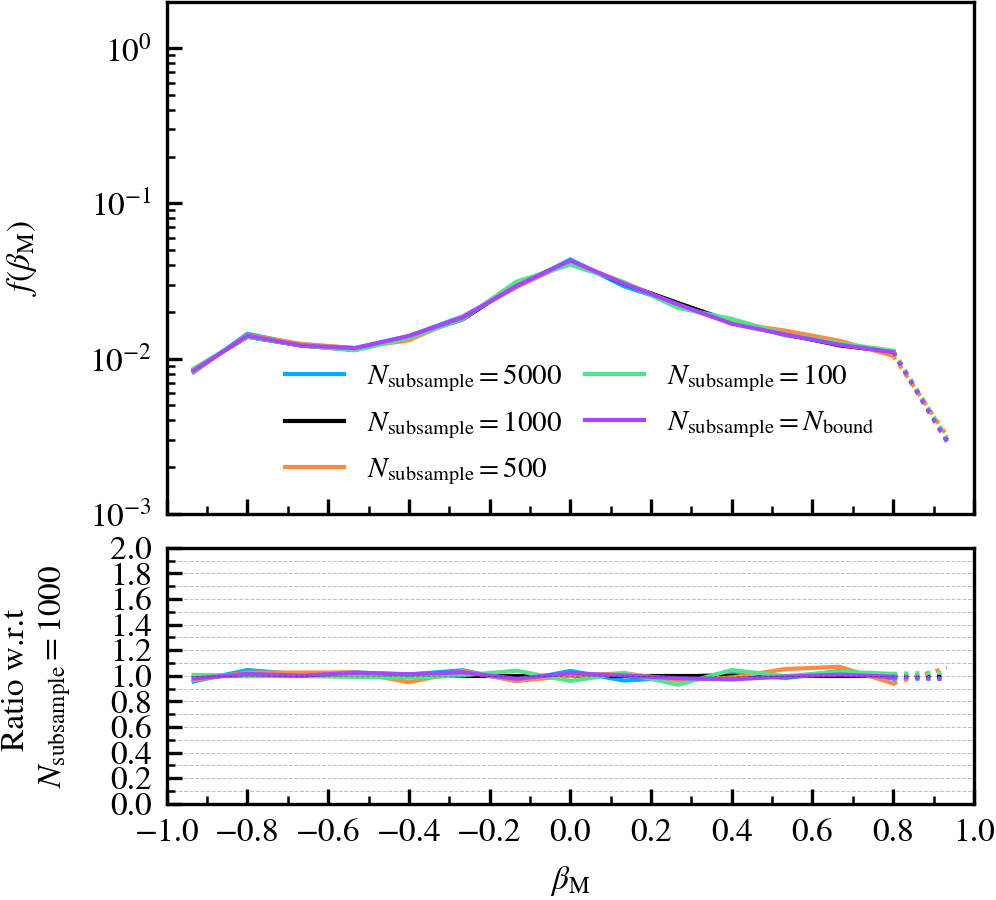
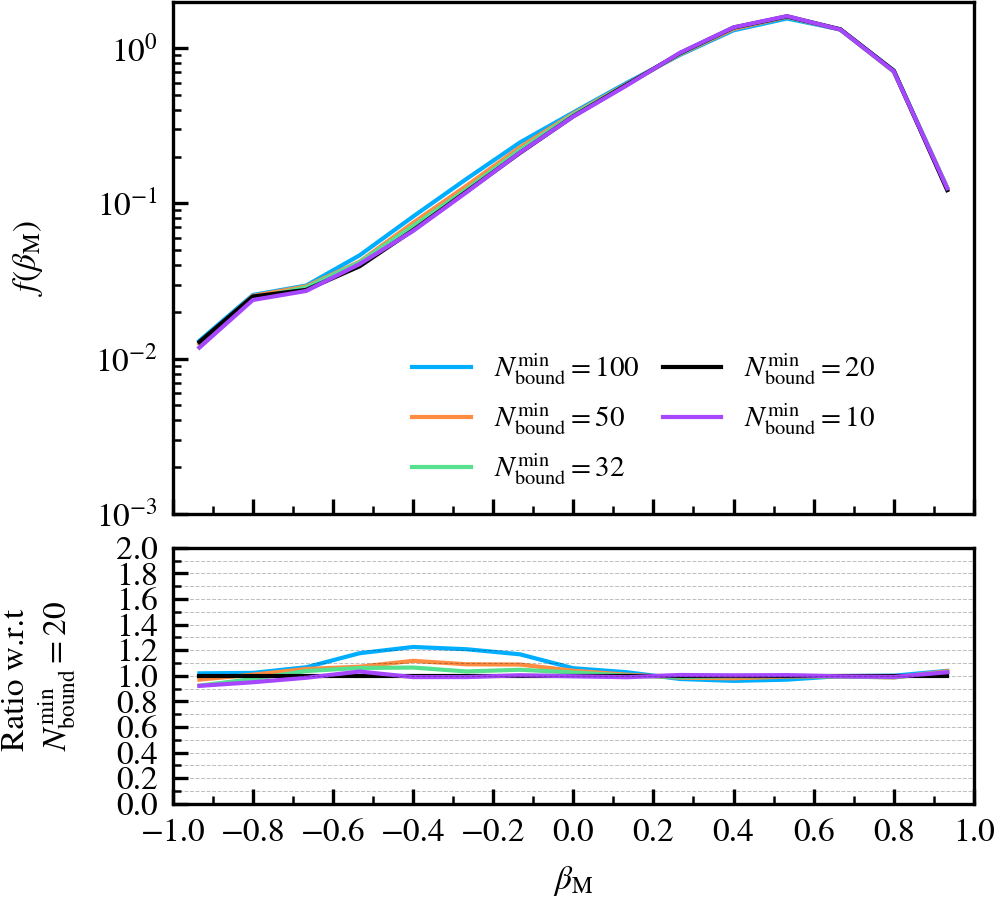
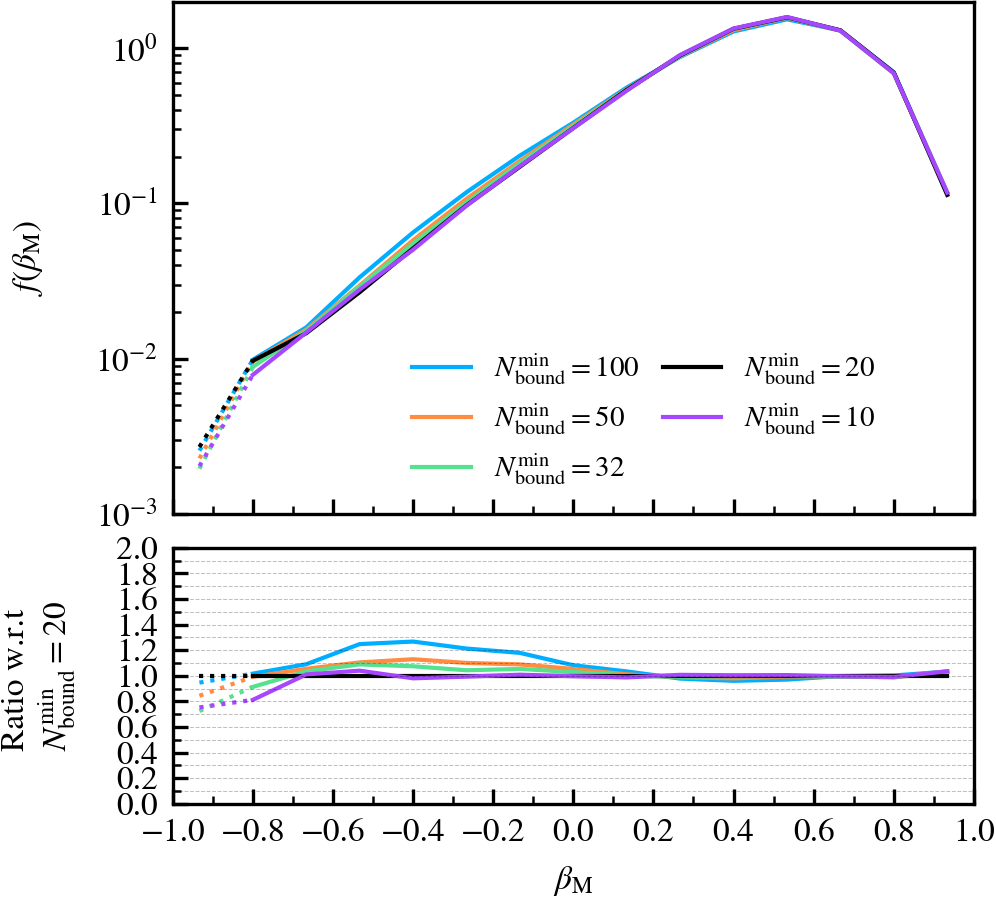
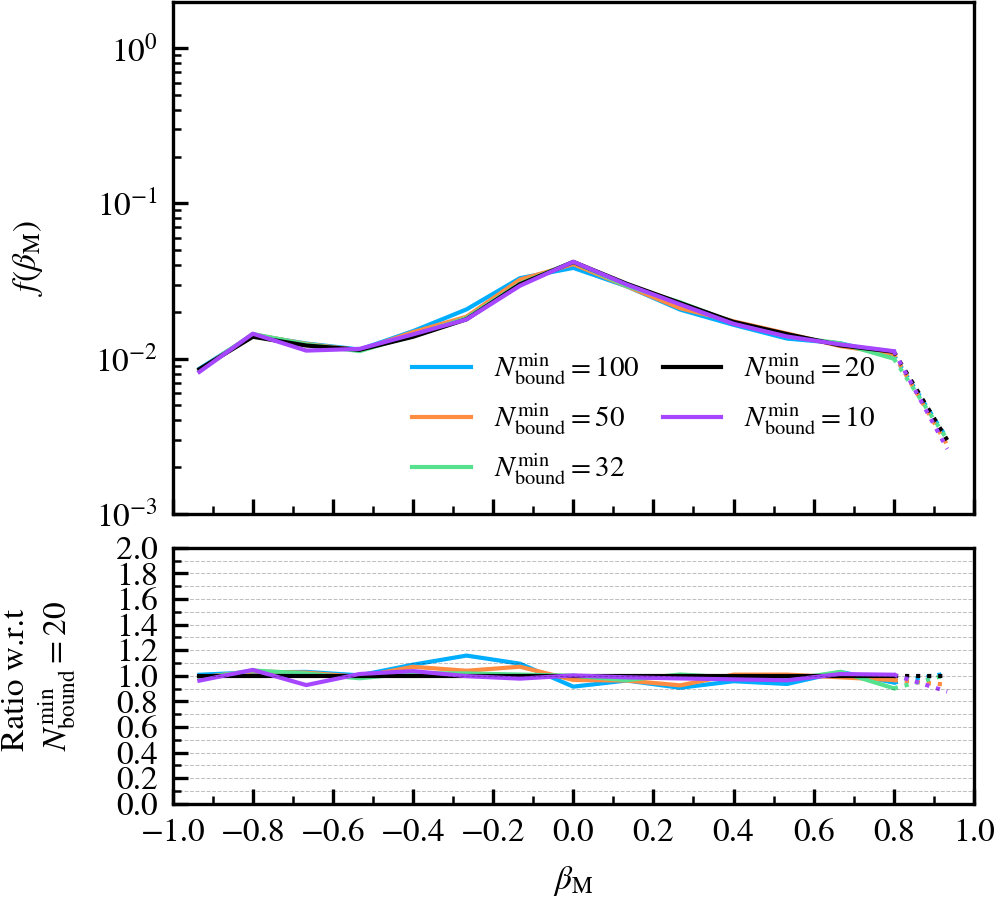
Length of the main progenitor branch ($L_{\rm progenitor}$): how long the main progenitor branch of self-bound subhaloes at $z = 0$ is. The central vs satellite classification is done based on the Depth value of the subhalo at $z = 0$, where Depth = 0 is a central subhalo and a satellite if Depth != 0. We further subdivide the subhalo population into three bins according to $M^{\rm z=0}_{\mathrm{bound}}$.
Normalised mass growth factor ($\beta_{\rm M}$): the normalised arctangent of the exponent coefficient describing an exponential mass growth of a subhalo between two consecutive outputs, i.e. $$ \beta_{\rm M} \equiv \dfrac{2}{\pi}\arctan\alpha_{\rm m} = \dfrac{2}{\pi}\arctan \dfrac{\ln [ M_{\rm bound}(z_{i+1}) / M_{\rm bound}(z_{i})]}{z_{i} - z_{i+1}}\,, $$ where $z_{i} > z_{i+1}$. We use subhaloes across all redshifts, but only if both $M_{\rm bound}(z_{i+1})$ and $M_{\rm bound}(z_{i})$ are above a threshold mass $M_{\mathrm{th}} = 6.72\,\times10^{13}\,\mathrm{M}_{\odot}$ ($10^{4}$ particles). The central vs satellite classification is done based on the Depth value of the subhalo at the two consecutive outputs under consideration. Thus, central subhaloes have Depth = 0 in both outputs and satellite subhaloes have Depth != 0 in both outputs instead.

Aside from these summary statistics, we also provide for certain parameters one or more supplementary plots, which are used to illustrate the effect that those parameters may have in a more direct manner.

Note

We always keep the y-axis limits consistent across panels that show the same property, regardless of the parameter variation being shown. If less than 100 subhaloes are present in a given bin, we use a dashed line to indicate the poor statistics at that x-axis value. We focus our discussion to the parameter ranges sampled by 100 subhaloes or more, except for illustrative purposes.

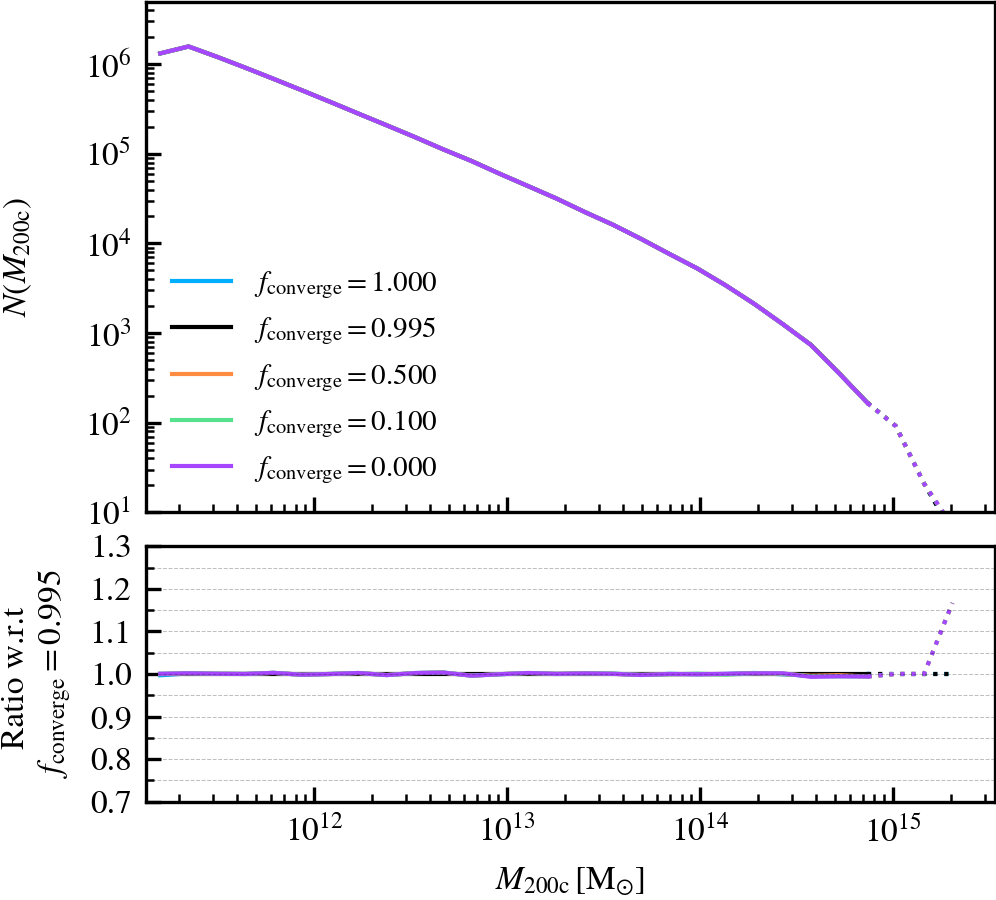
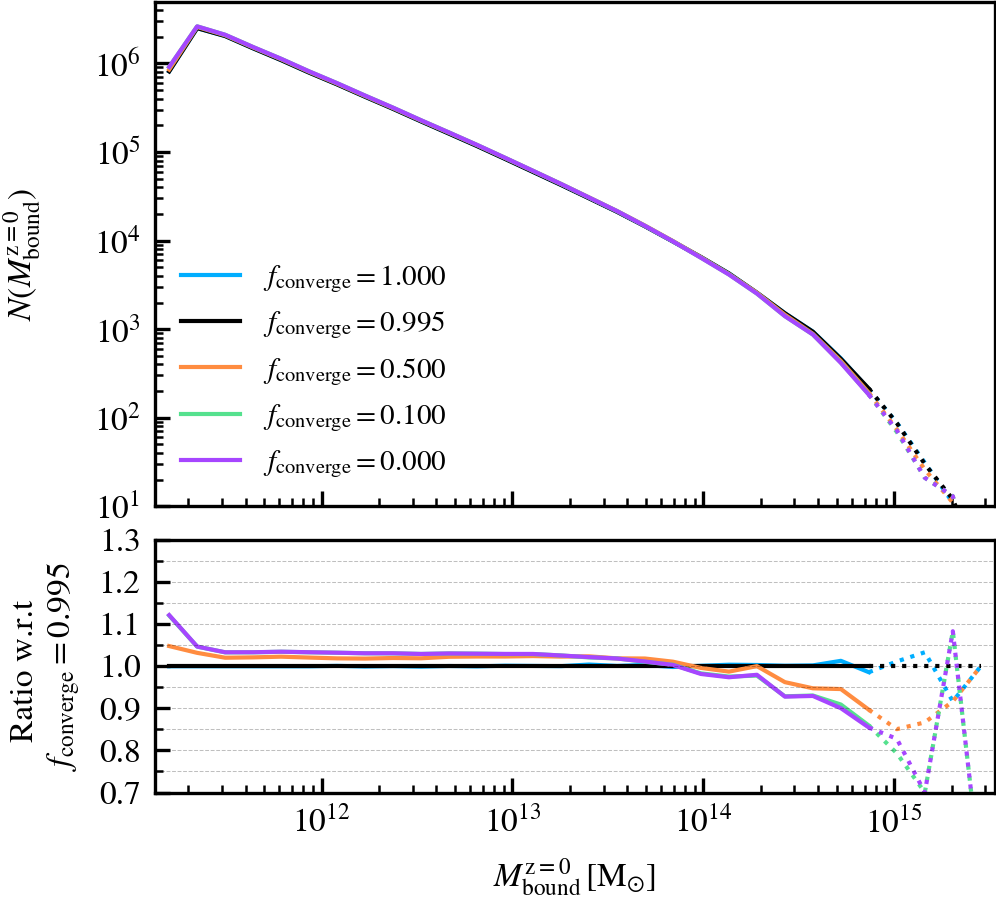
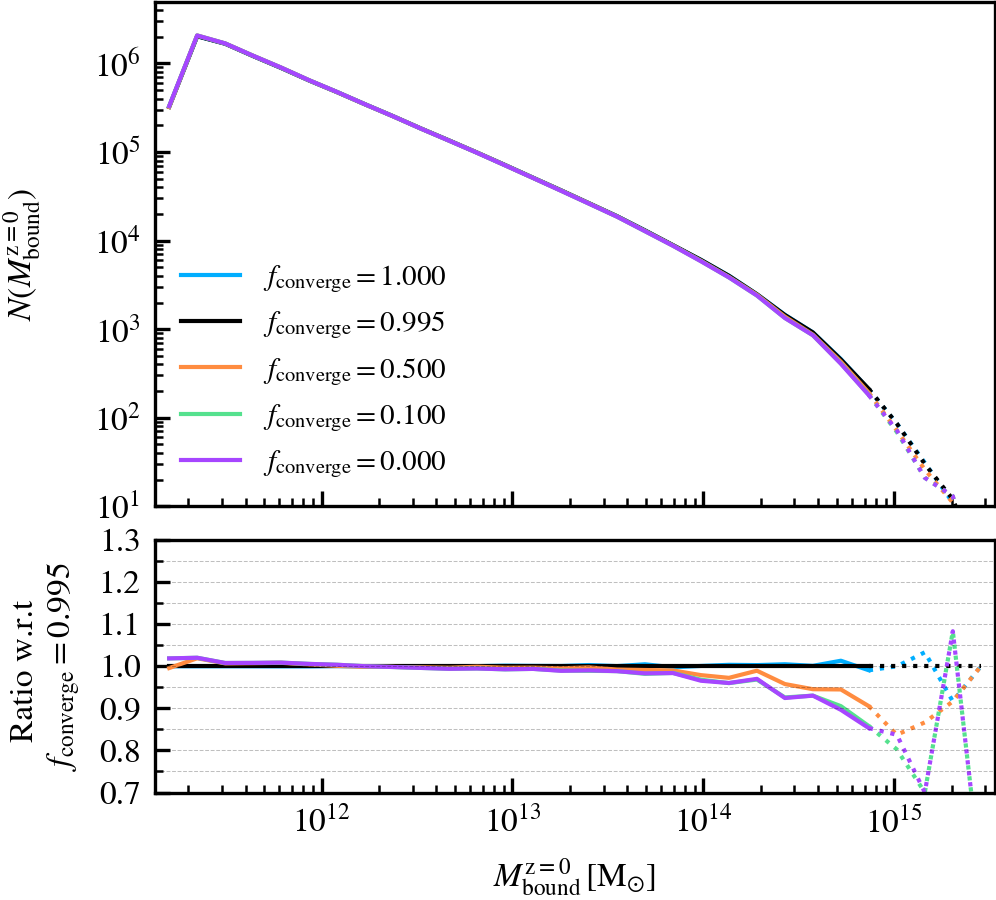
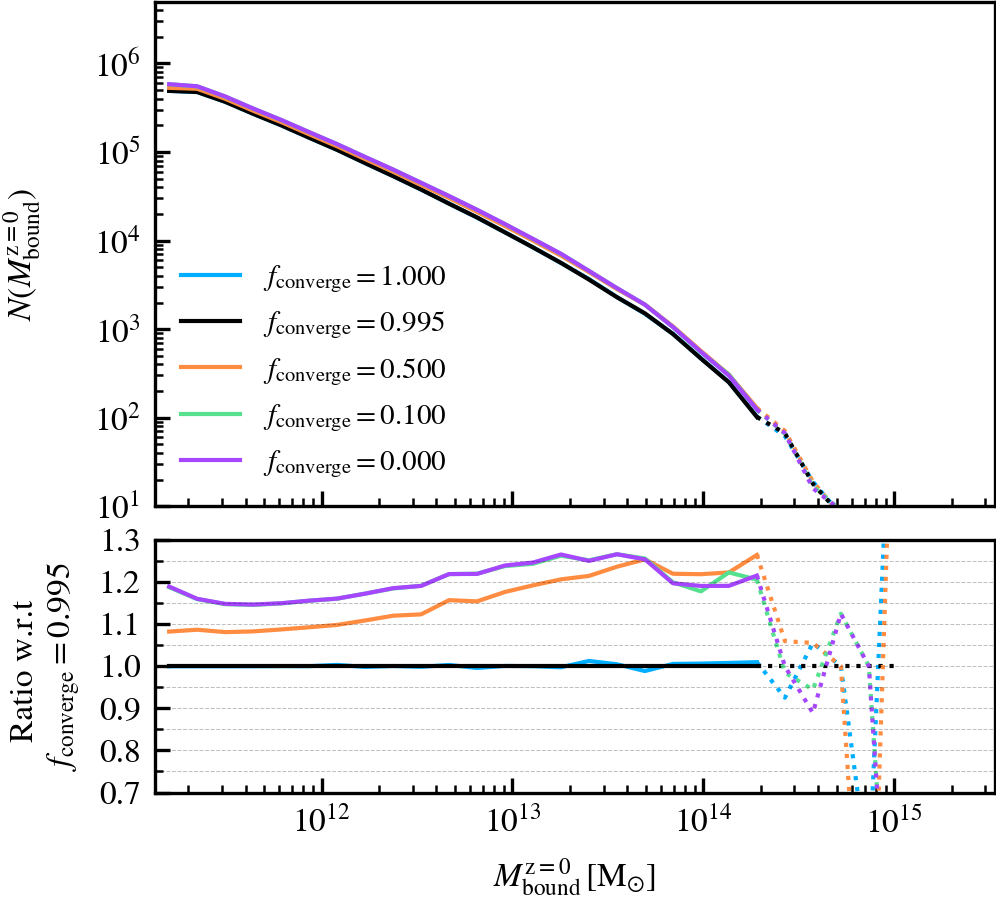
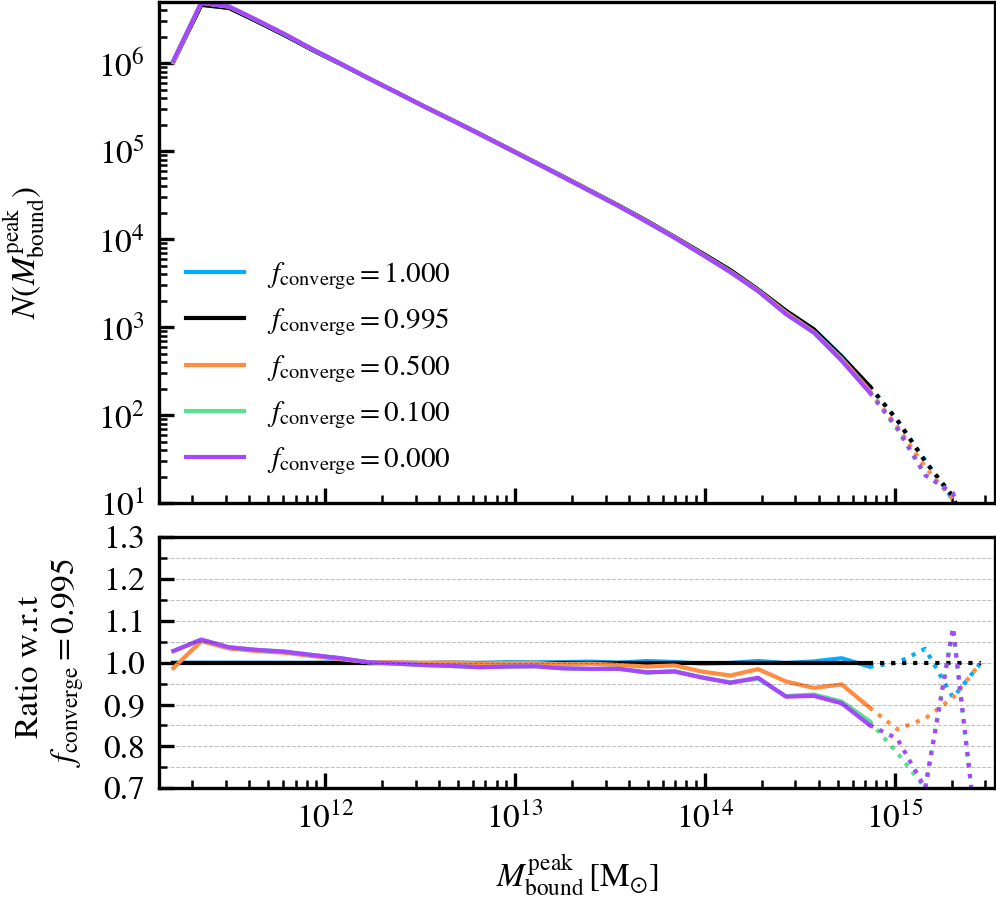
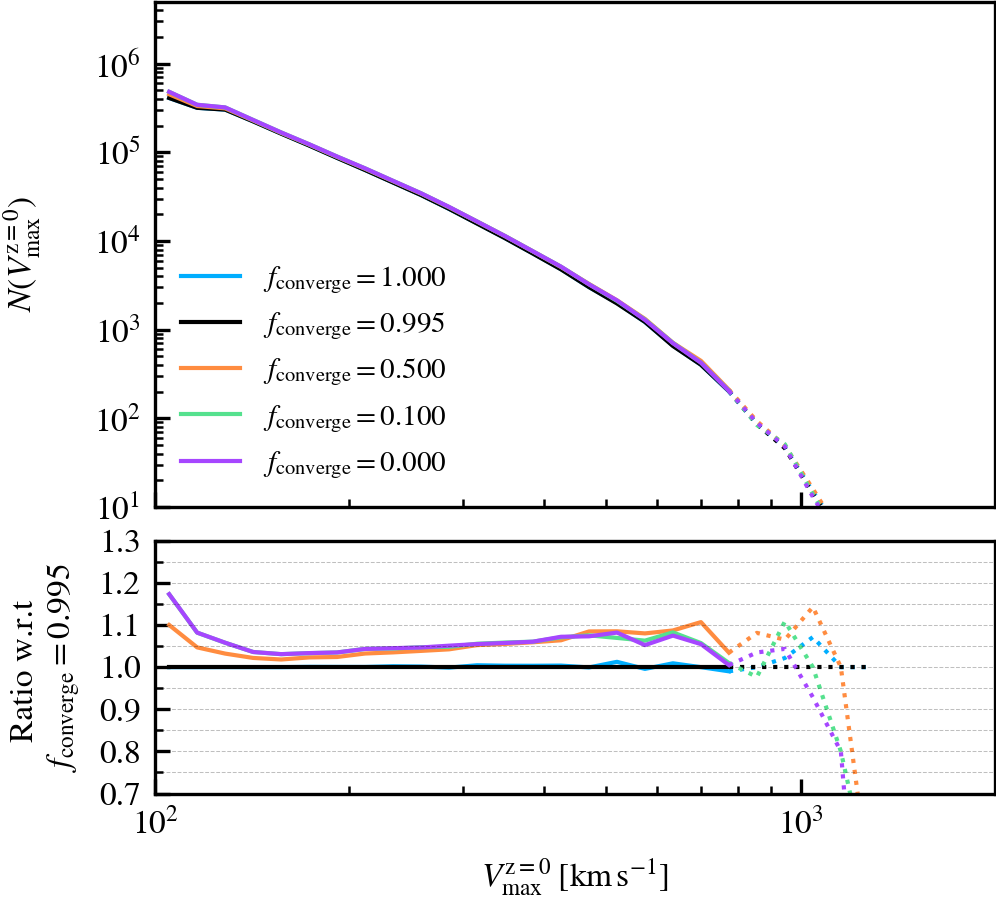
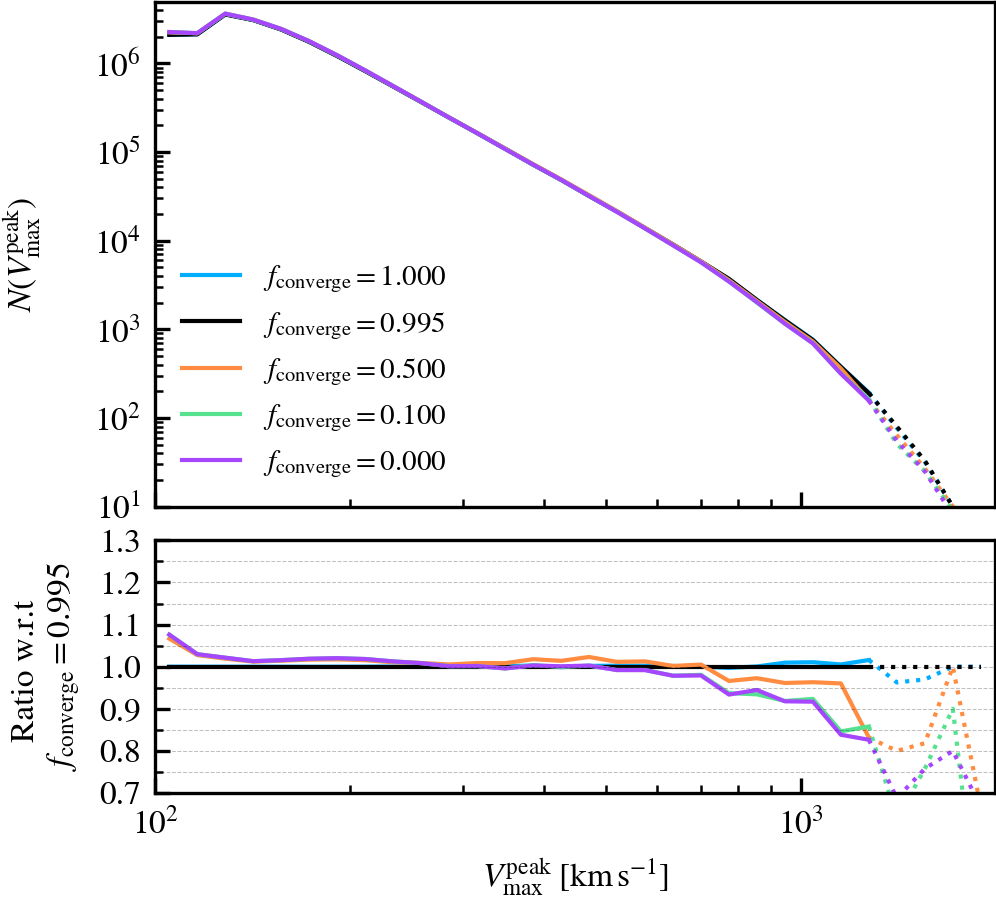
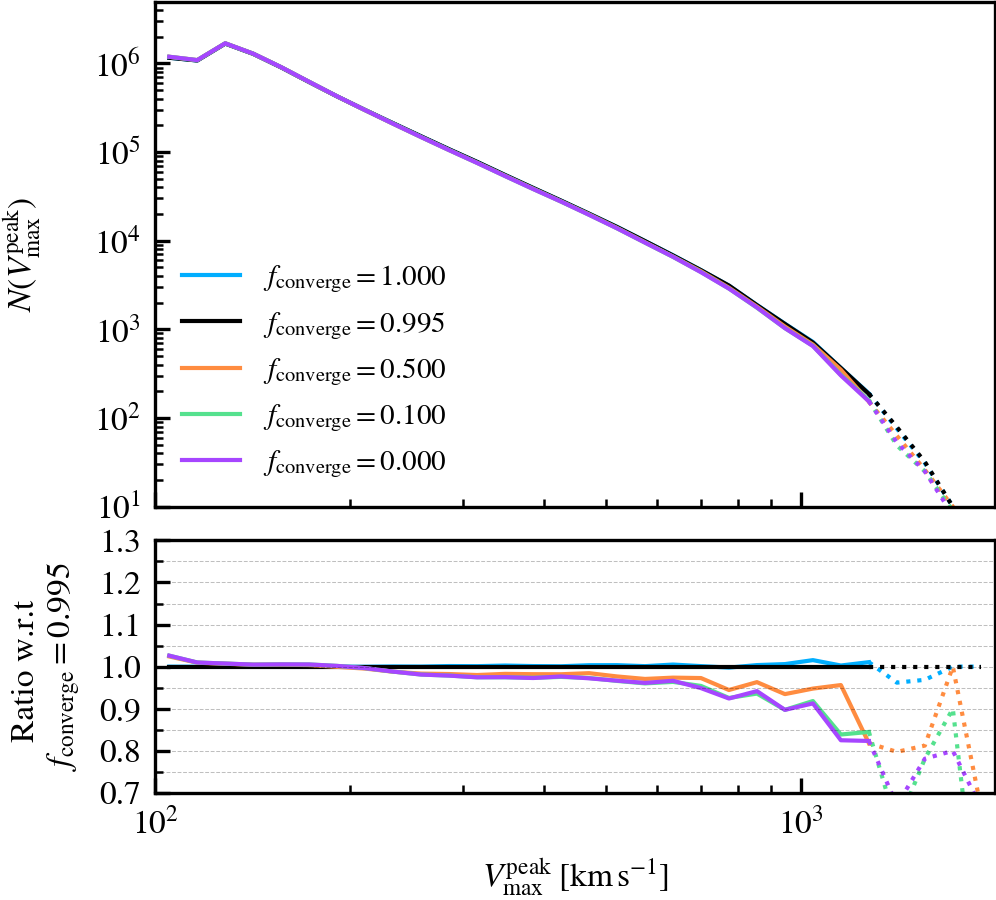
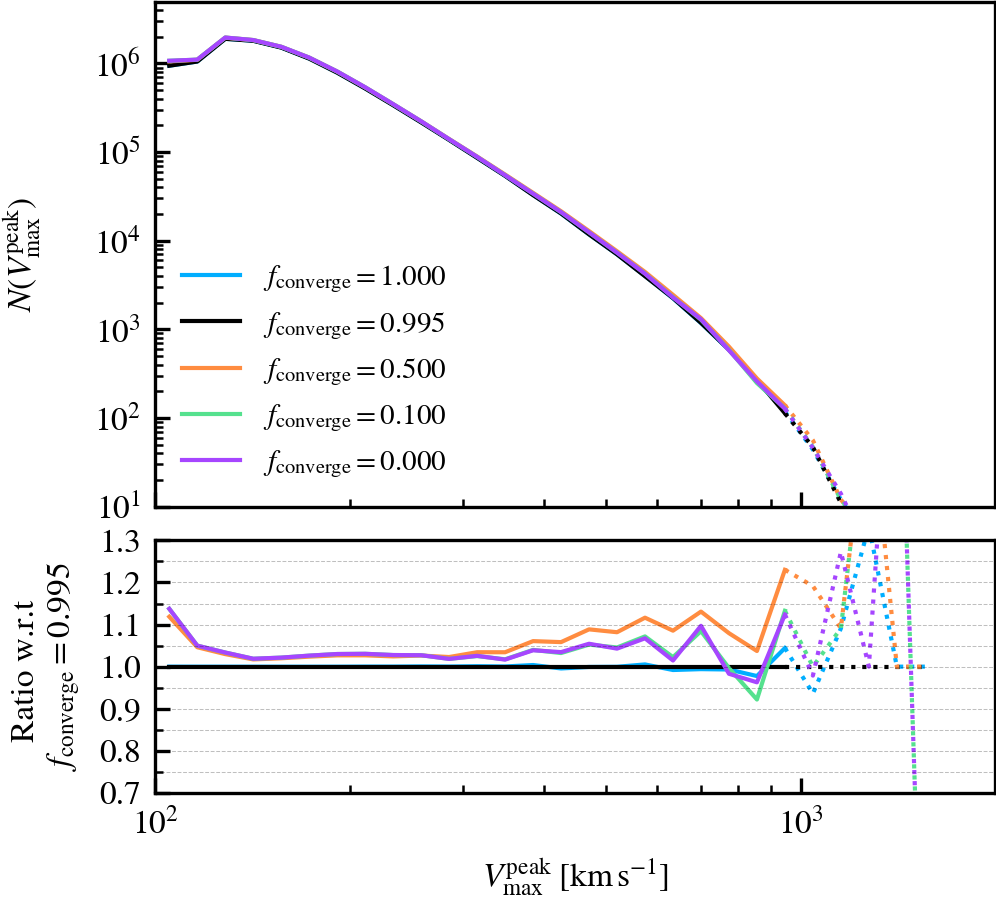
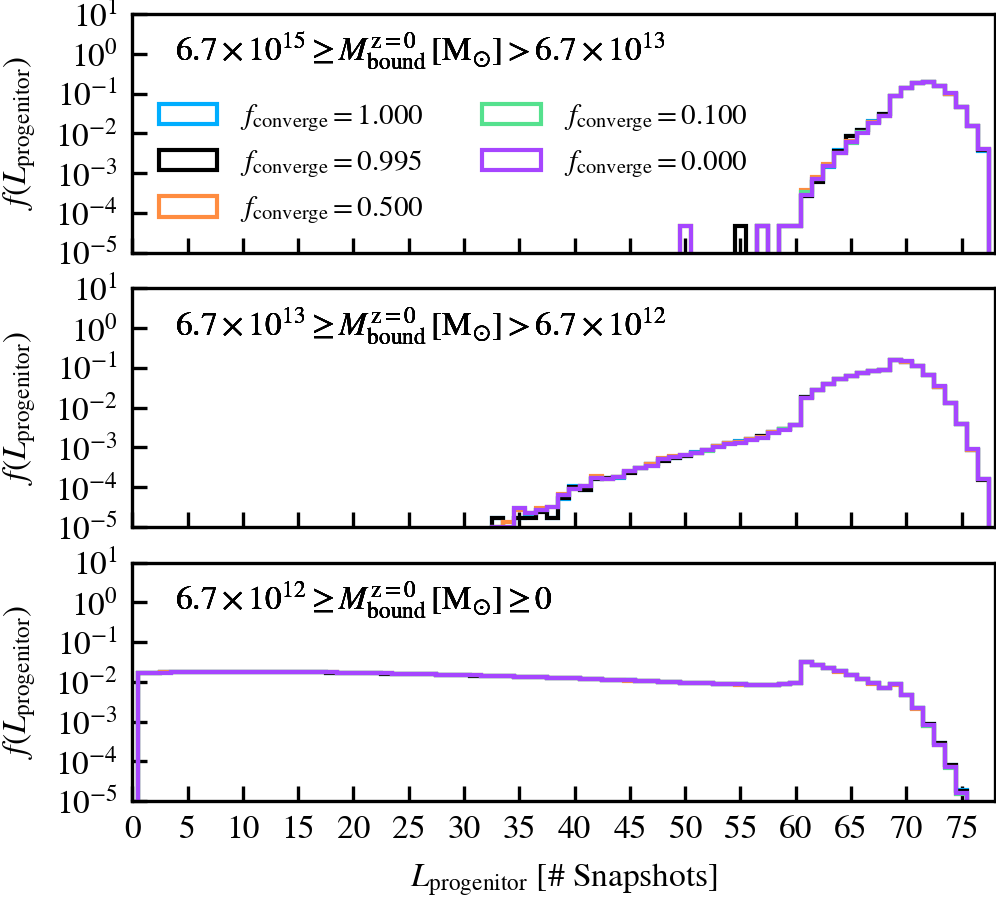
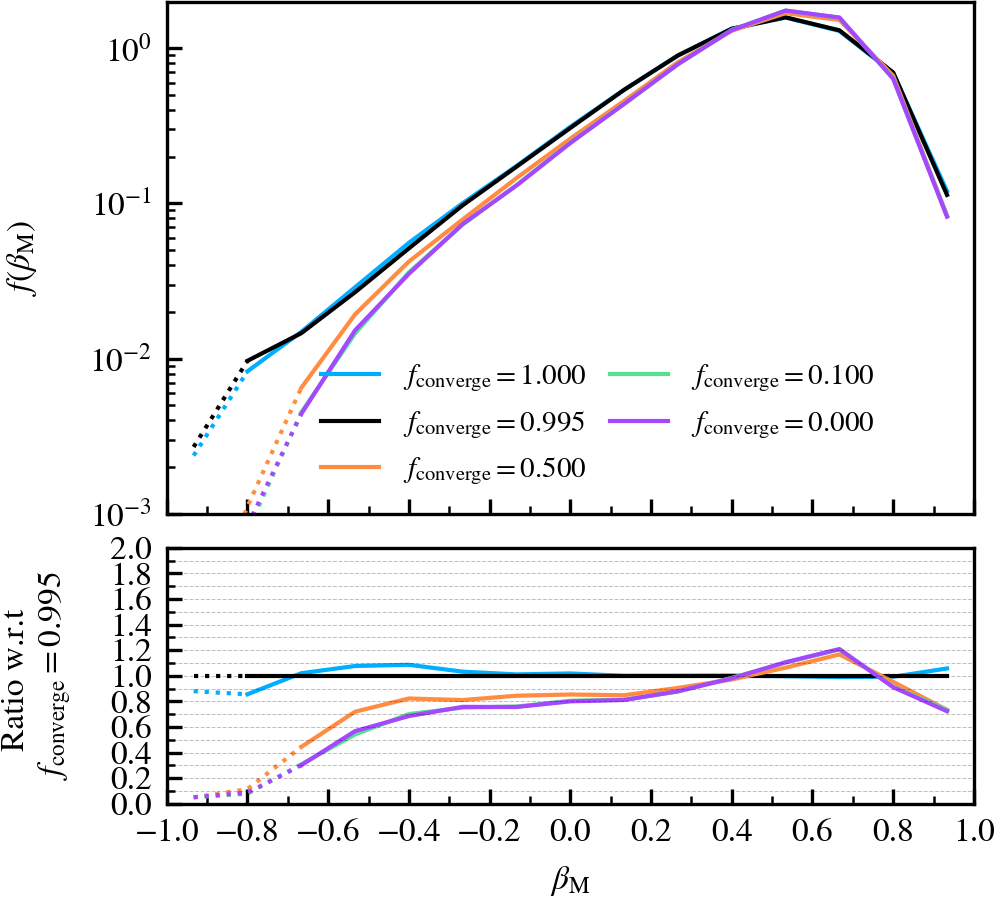
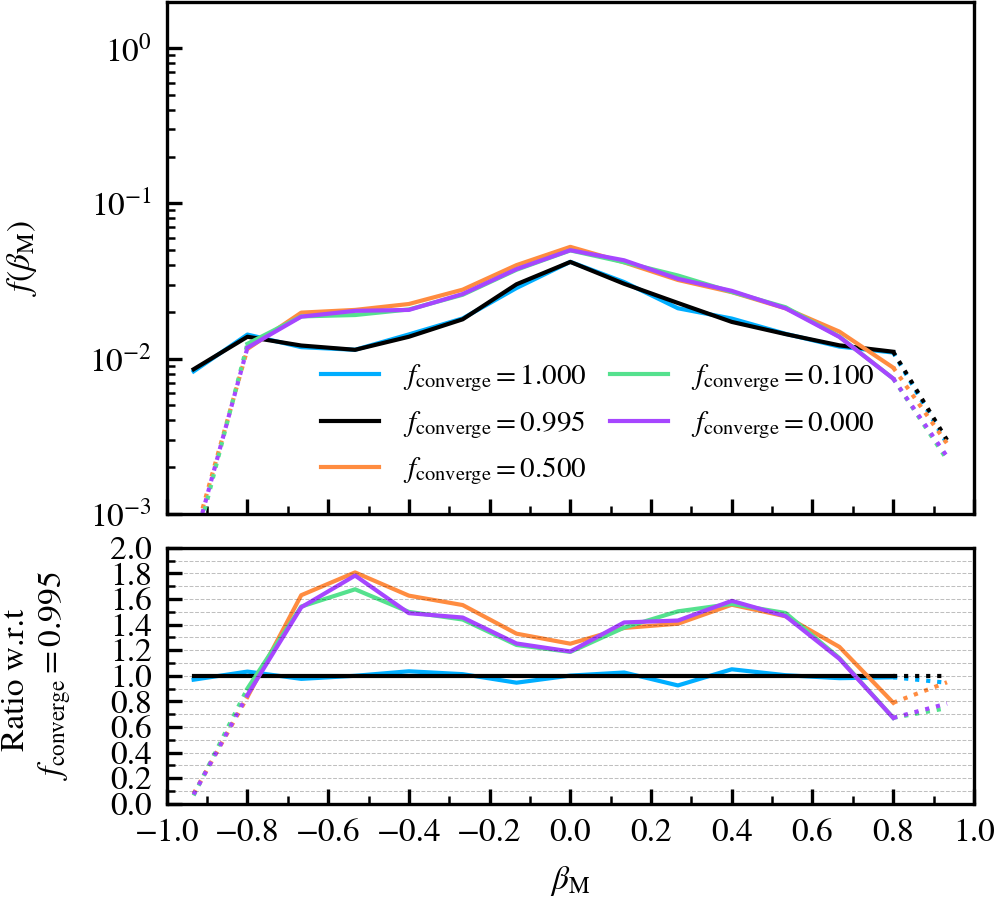
`BoundMassPrecision`

This parameter, which defaults to $f_{\rm converge} = 0.995$, regulates the threshold used to determine whether subhalo unbinding has converged or not. Lowering the value thus results in a more lax condition of convergence, and hence less overall unbinding iterations being done. Since in each consecutive iteration a subhalo can only lose (unbound) mass, less iterations generally result in systematically more massive subhaloes, depending on the subhalo depth. As mass is assigned exclusively and in a depth-first manner, satellite subhaloes preferentially gain more mass than the default, whereas centrals become less massive due to the exclusion of mass they would have otherwise accreted.

We recommend using a sufficiently high value so that subhaloes are subject to at least one unbinding iteration, i.e.somewhere in the range between $f_{\rm converge} \in [0.9,1]$. For computational cost purposes, we advise not to use exactly a value of one. This will re-trigger a whole unbinding iteration even if a single particle is found to be unbound. For objects with large numbers of particles, this can get expensive even though it makes no practical difference to the subhalo properties. Using a low value will speed up the unbinding, but it will result in unbound mass being incorrectly classified as bound. The default choice of $f_{\rm converge} = 0.995$ results in properties that agree well with the most restrictive parameter value of $f_{\rm converge} = 1$.

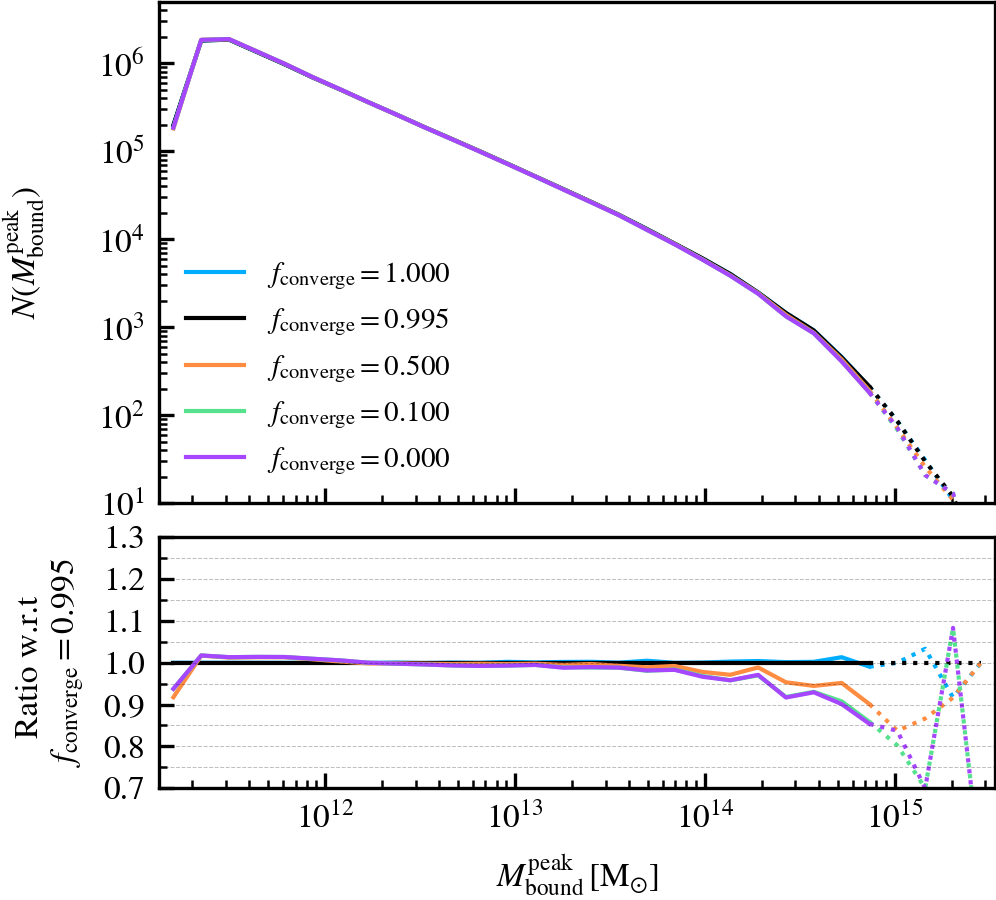
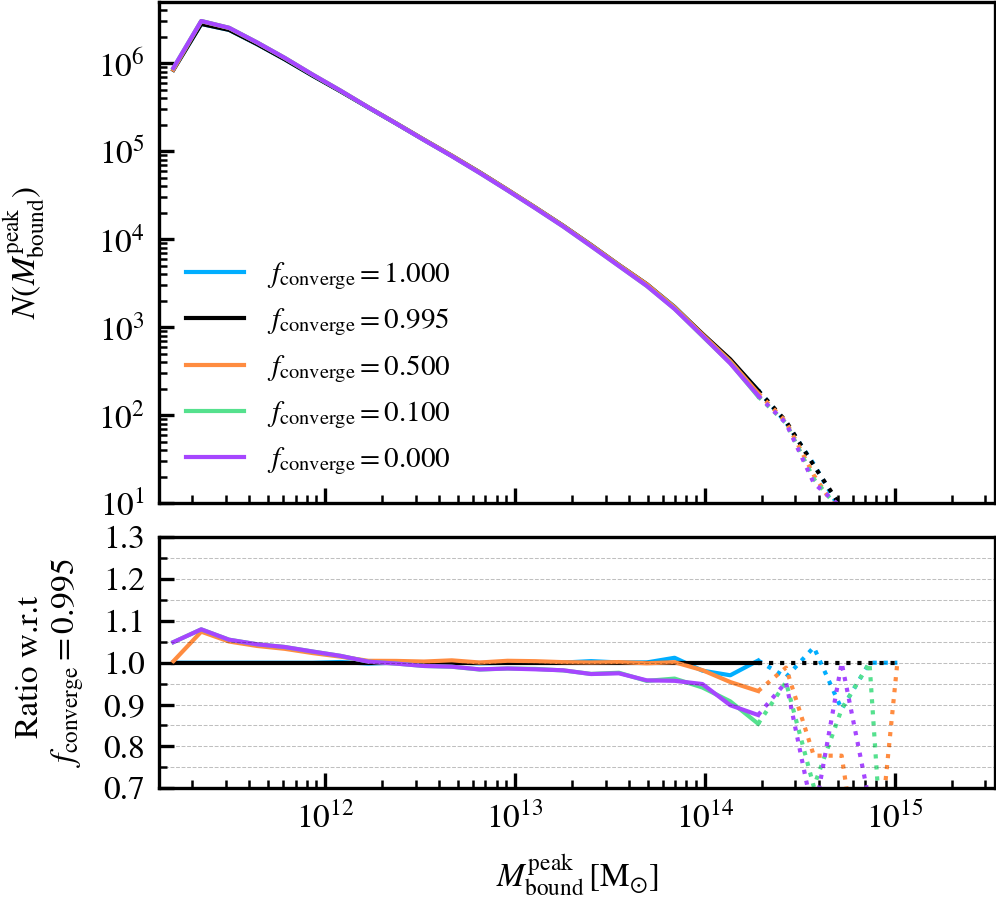
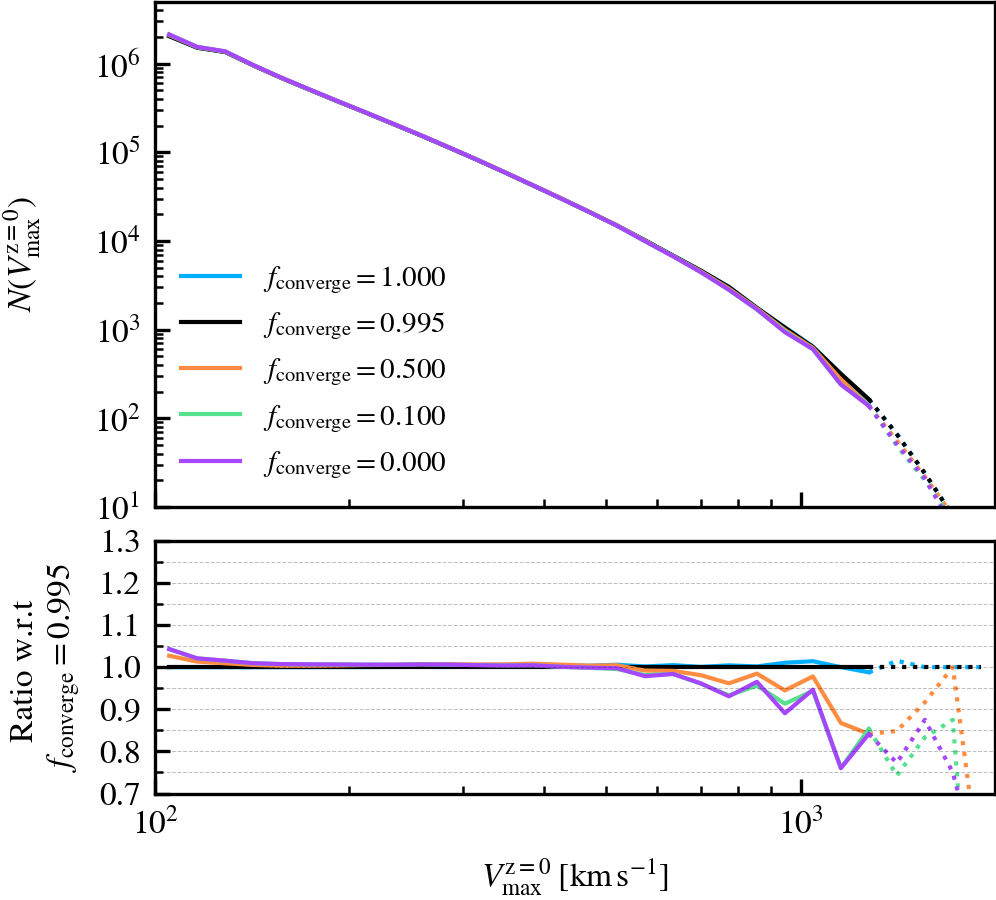
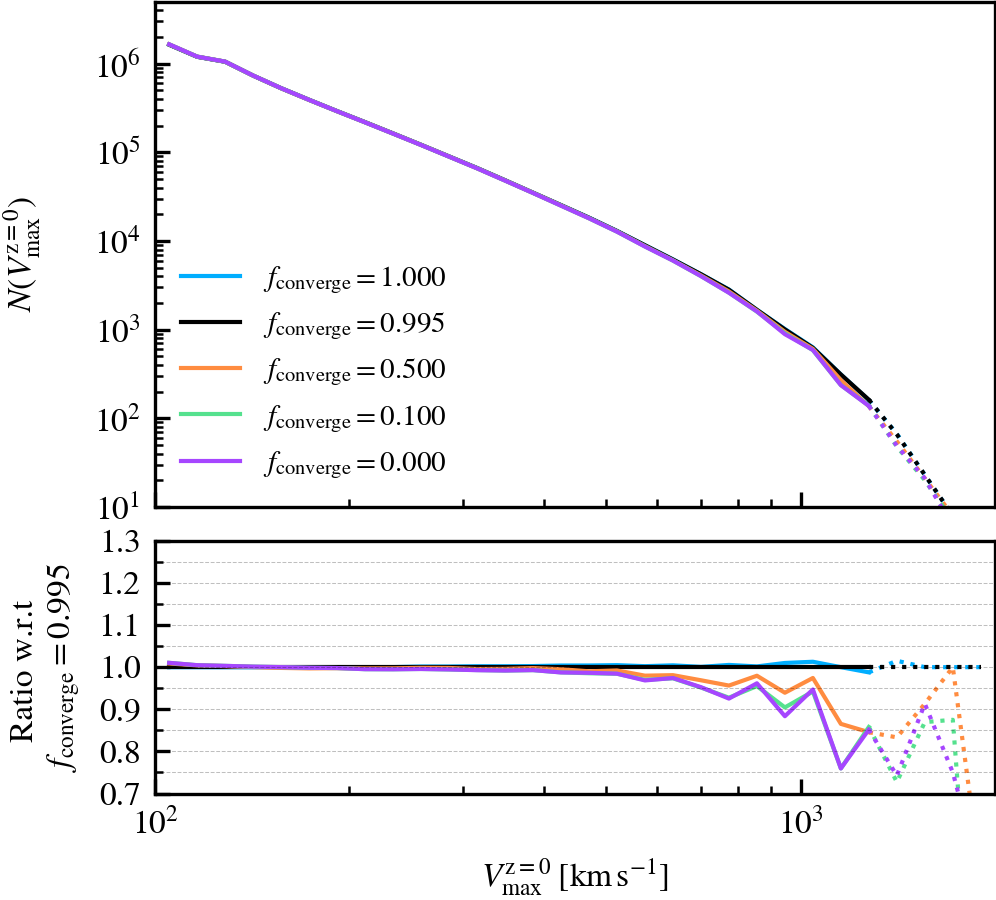
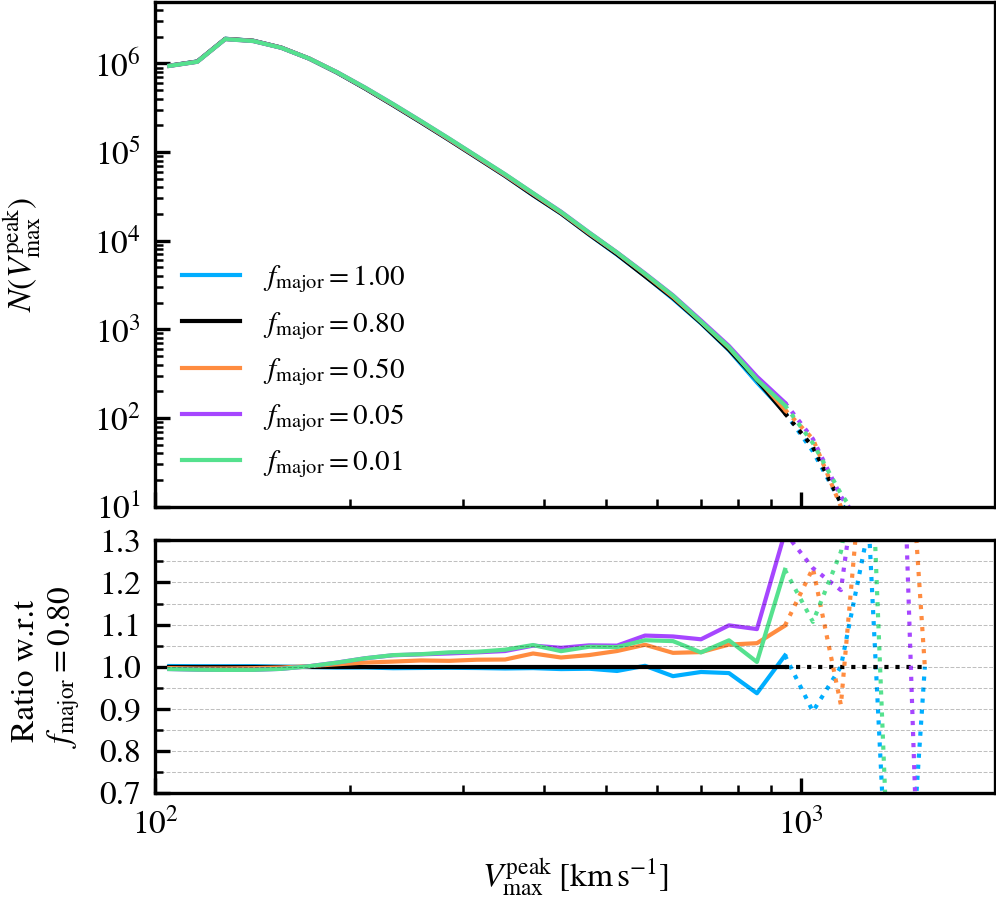
`MajorProgenitorMassRatio`

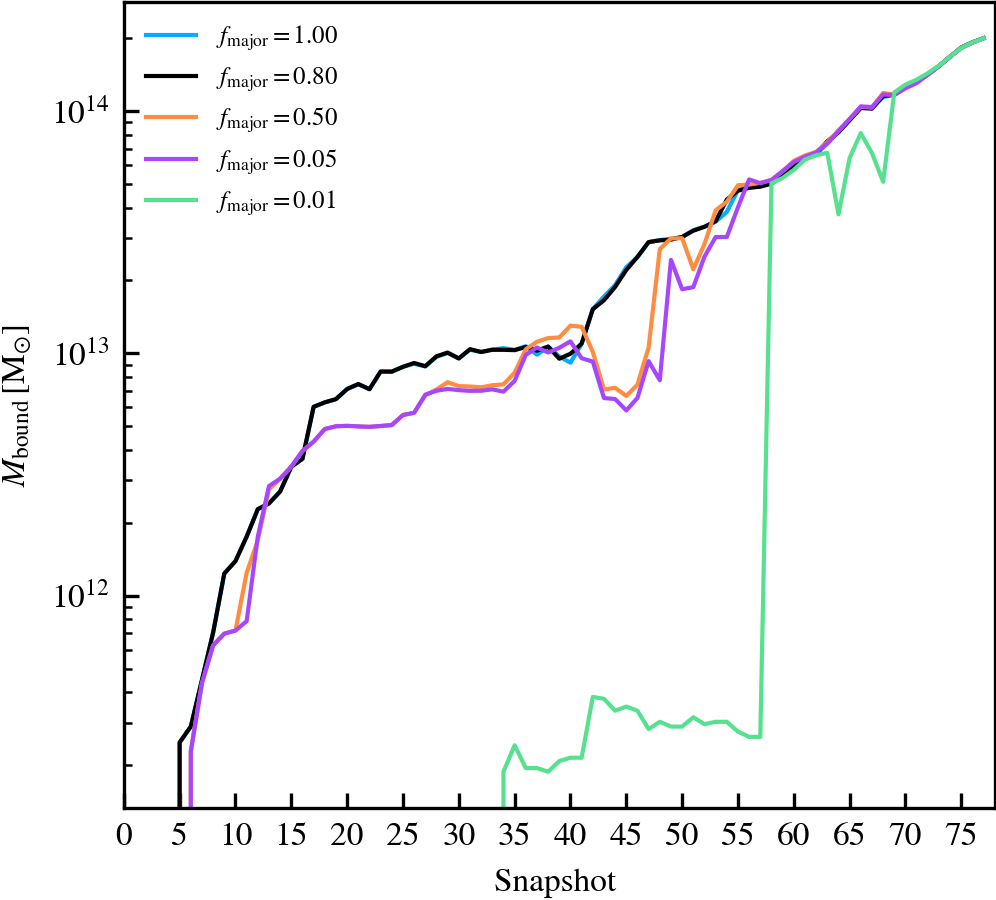
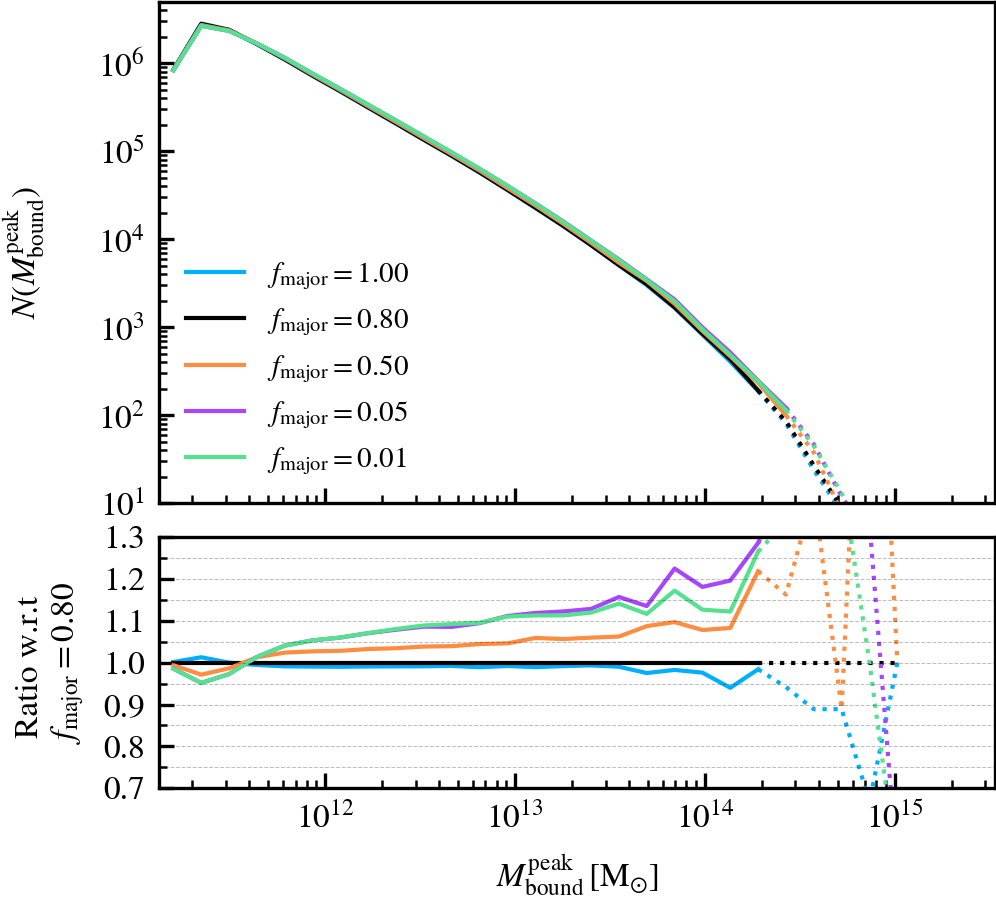
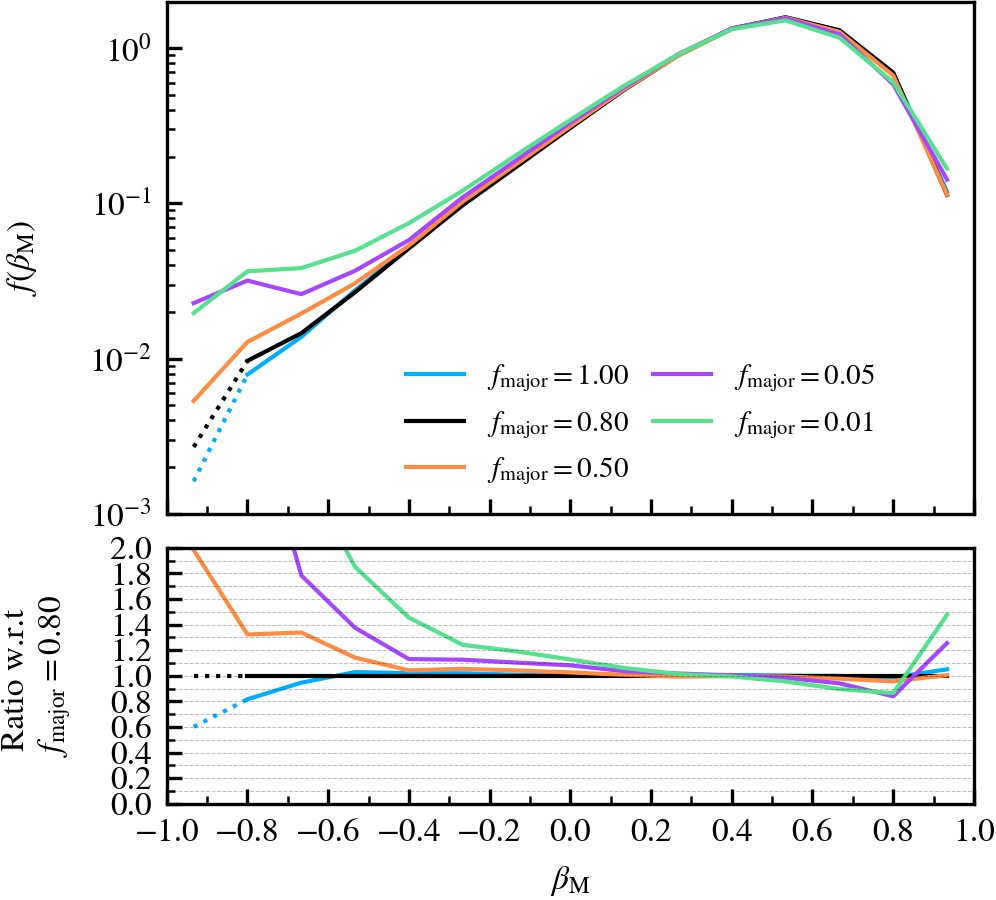
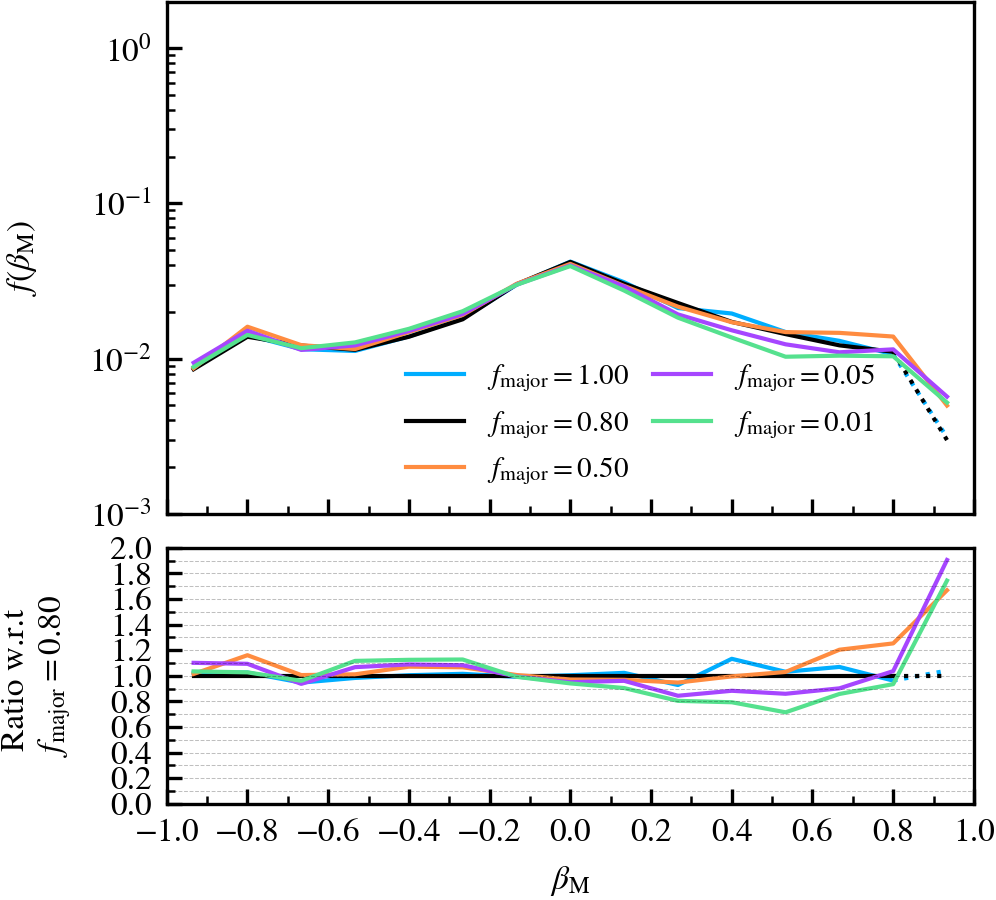
This parameter, which defaults to $f_{\rm major} = 0.8$, determines the mass threshold (expressed relative to the subhalo with the largest mass in the previous output) above which subhaloes in a FoF group will be considered to be a central subhalo candidate. The central subhalo will be chosen among the pool of central subhalo candidates, based on the one with the lowest orbital specific kinetic energy in the centre of mass frame of their host FoF group. Lowering the value increases the number of central subhalo candidates, with a value of $f_{\rm major} = 1$ forcing the choice to be the subhalo which was the most massive in the previous output.

We recommend not lowering the value below $f_{\rm major} = \mathcal{O}(0.1)$, as low mass subhaloes become eligible to be centrals. Since they are more abundant than more massive subhaloes, it becomes increasingly likely to pick a low mass subhalo as a central instead of a more "adequate" massive subhalo. The supplementary plot shows an example where this happens, which leads to wild variations in mass. Conversely, we do not recommend using a value of $f_{\rm major} = 1$, since it would be too restrictive during the selection of a central subhalo. For example, two central subhaloes with the same $M_{\rm 200c}$ but different amount of mass in satellites would make the code choose the one with least mass in satellites (recall that mass is assigned exclusively).

However, we note that the choice of central is not solely determined by the combination of the mass threshold and orbital kinetic energy criterion. If after unbinding it turns out that the central subhalo identified during this step is not the most massive subhalo in the host FoF group, the central is changed to be the most massive. However, the accretion of particles in that output would reflect the originally incorrect central choice.

Supplementary plot

`MaxSampleSizeOfPotentialEstimate`

This parameter, which defaults to $N_{\rm subsample} = 1000$, is the maximum number of particles used in the gravitational tree to compute the gravitational potential of particles. If a subhalo has more particles than $N_{\rm subsample}$, a random subset of $N_{\rm subsample}$ particles is chosen from the current set of bound particles. The masses of the particles chosen in the subsampling step are upscaled by a factor that ensures the total mass of the system is conserved.

We recommend using a non-zero value of $N_{\rm subsample}$ as it speeds up the unbinding of subhaloes, which is one of the most costly parts of subhalo finding. However, the value should not be tiny, since the code becomes more likely to choose a subset of particles that do not represent the true mass distribution of the subhalo. For example, idealised N-body simulations analysed using $N_{\mathrm{subsample}} = \mathcal{O}(10^{1})$ reveal that subhaloes with $N_{\rm bound} \approx 10^{6}$ can be prematurely disrupted as a consequence of an unlucky choice subsampled set of particles. We consequently advise the user to carefully consider how many particles the best resolved subhalo in their simulation is expected to have, as the fraction of particles chosen at random will depend on ratio of $N_{\rm subsample}/ N_{\rm bound}$.

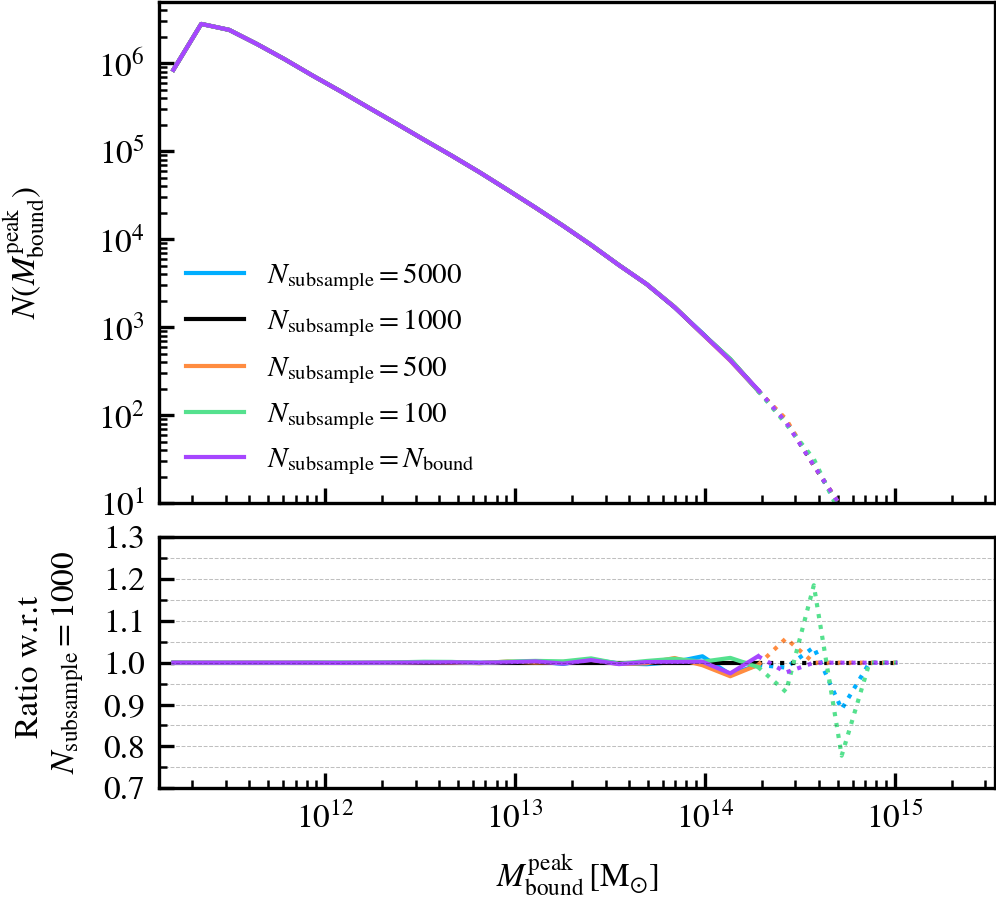
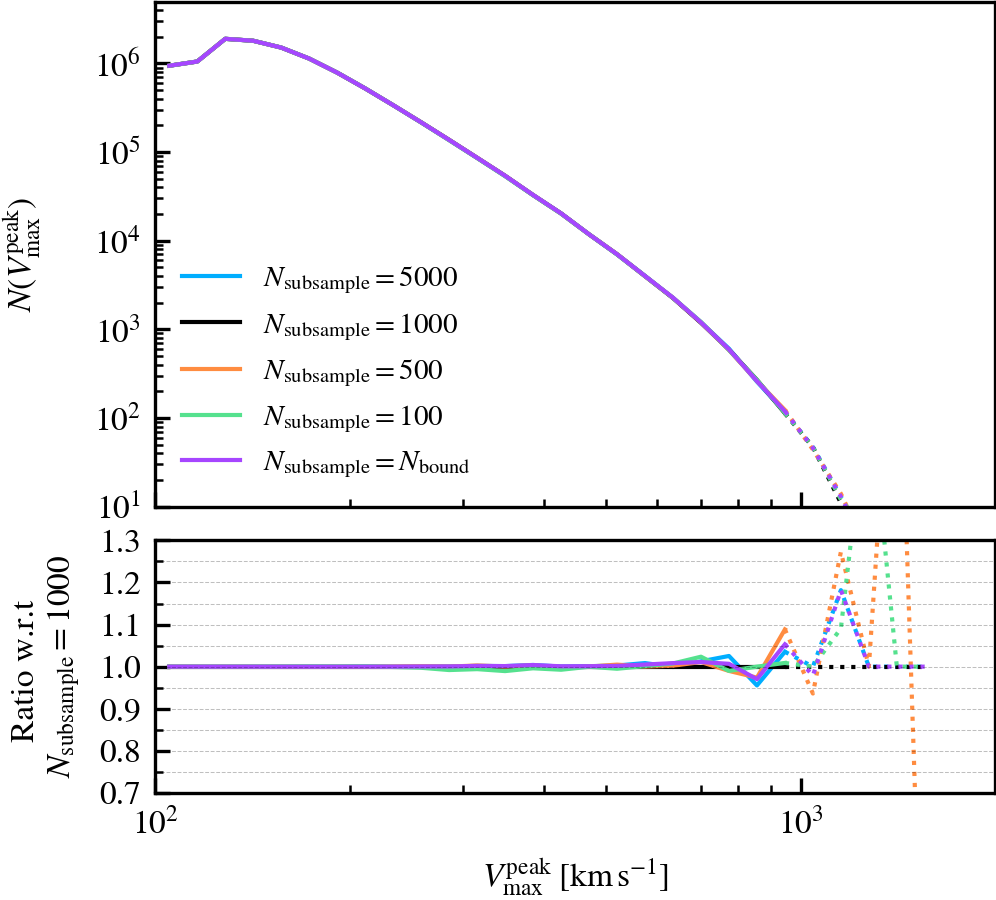
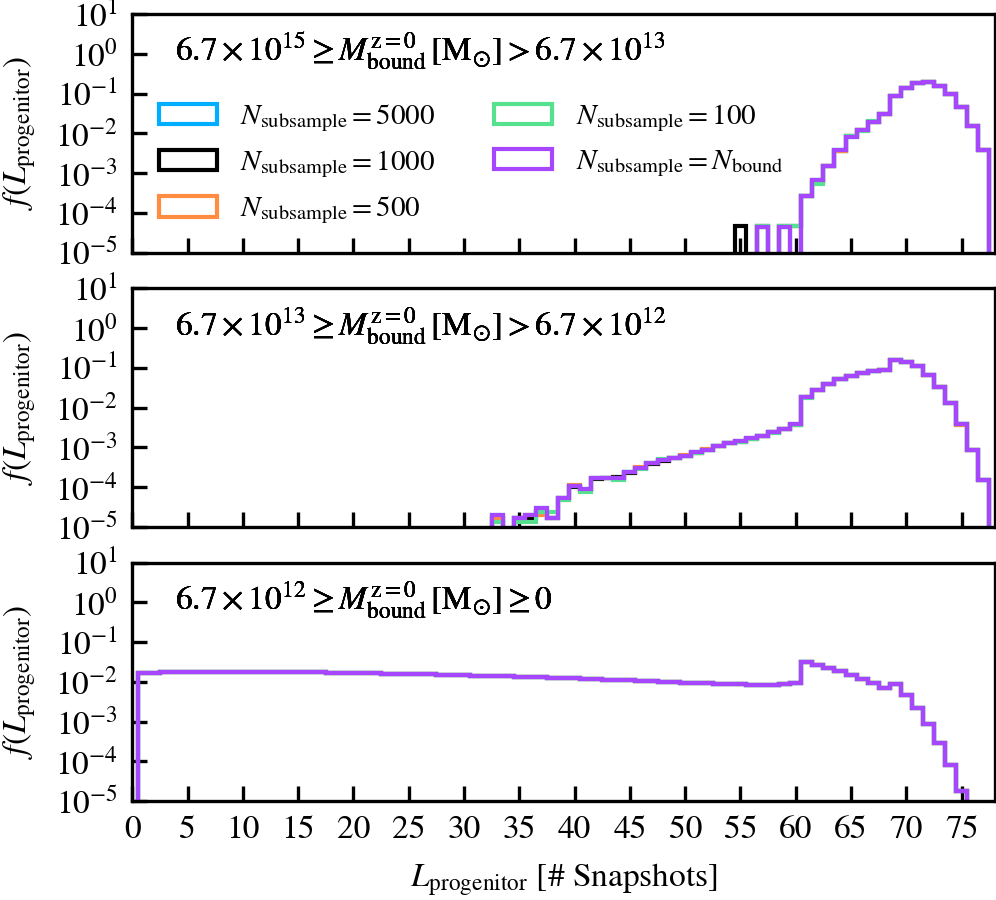
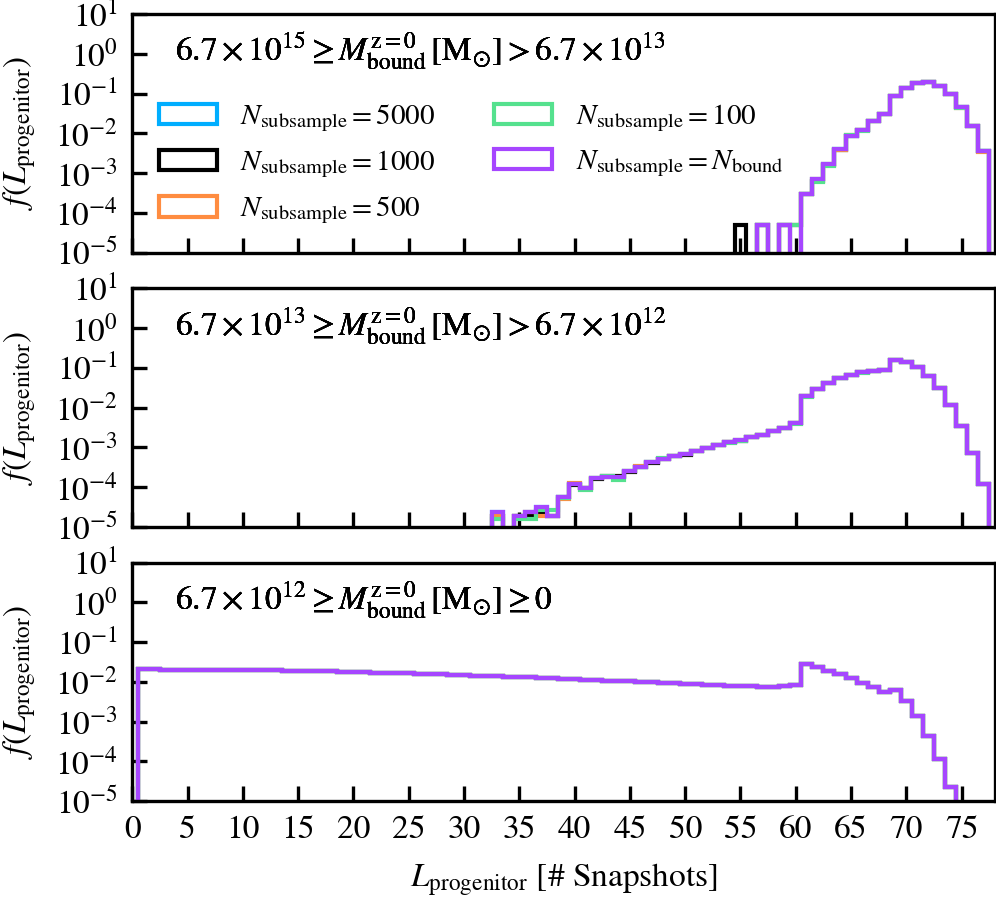
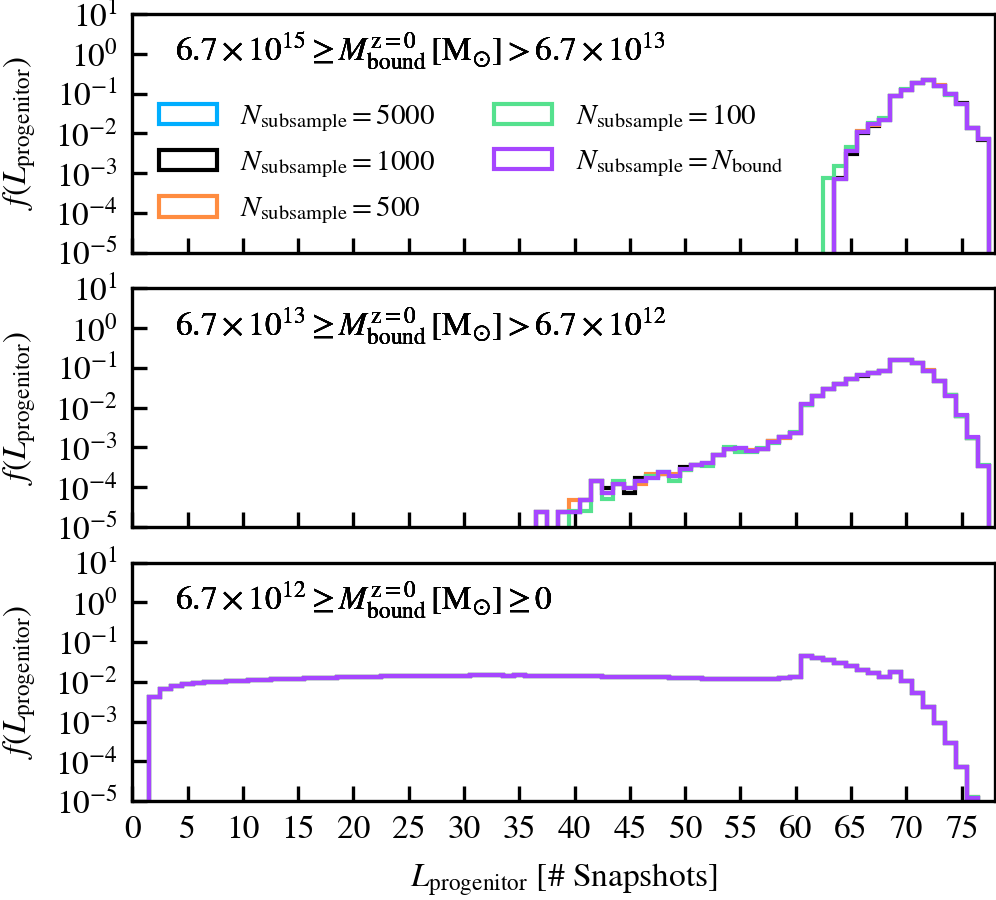
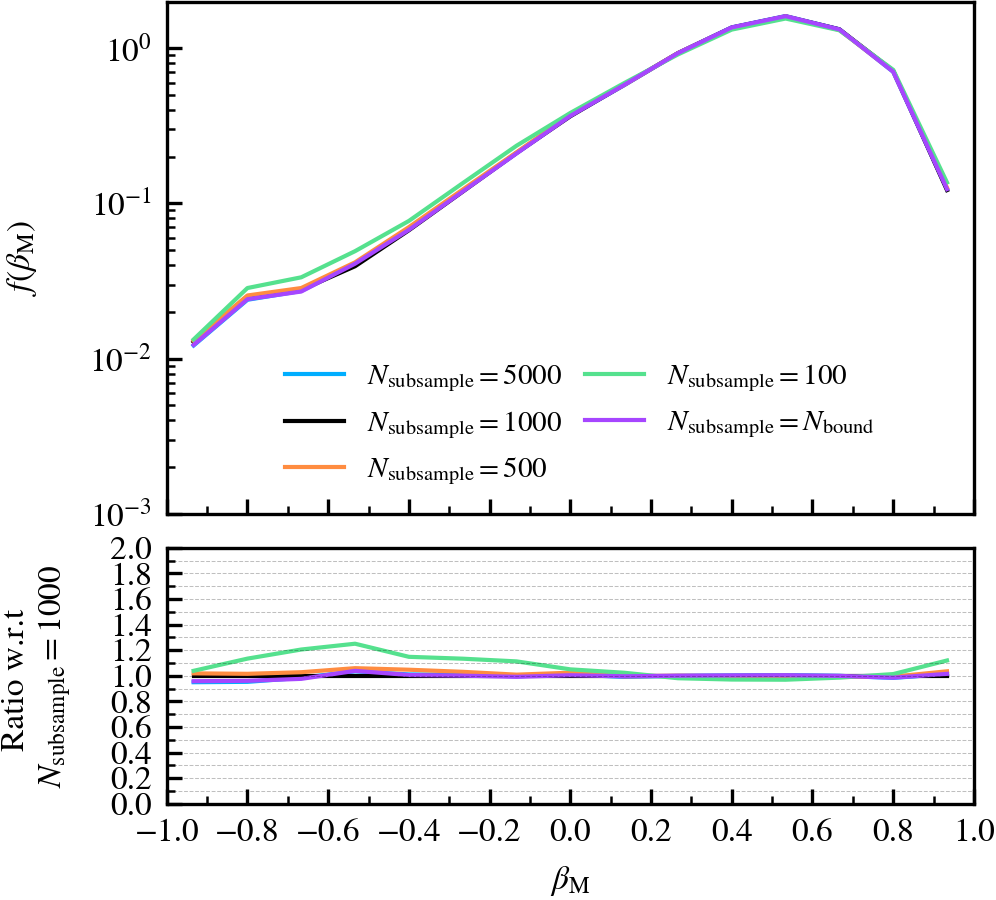
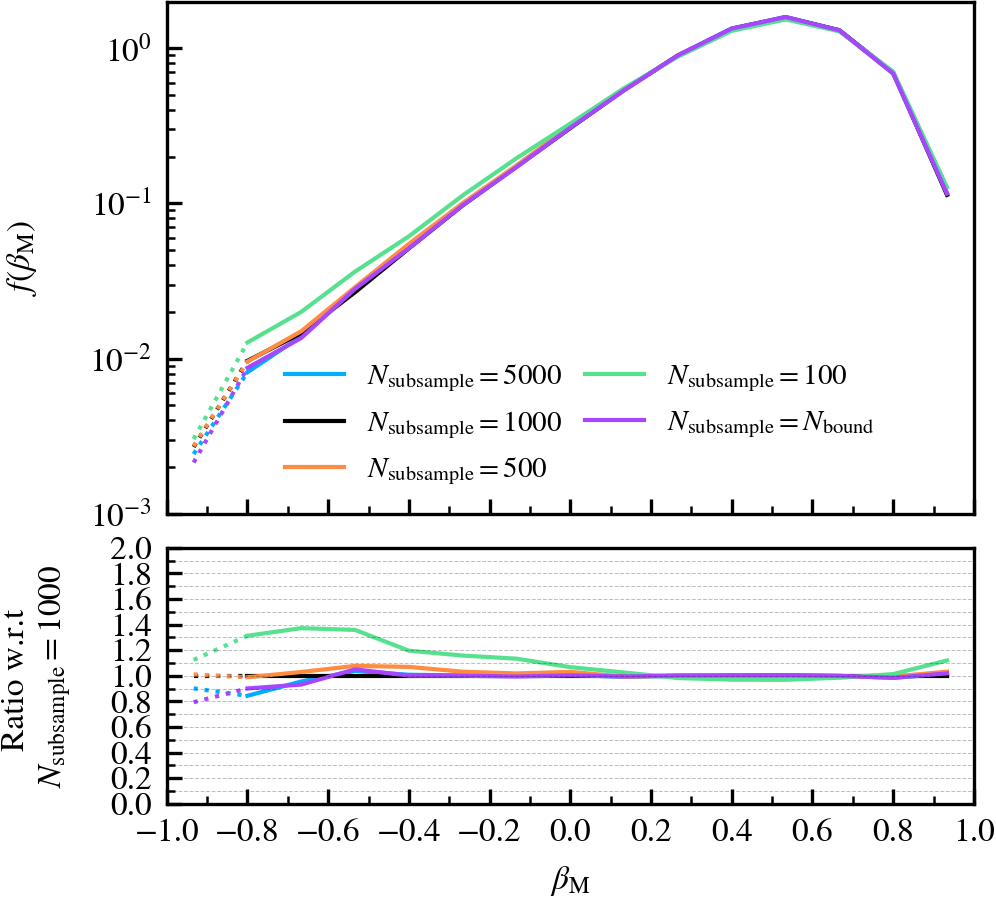
`MinCoreSize`

This parameter, which defaults to $N^{\rm min}_{\rm core} = 20$, determines the number of most bound particle tracers used to compute the phase-space coordinates and dispersion of self-bound subhaloes. Increasing the value means that more tracer particles (with lower binding energies) are included in the calculation, which primarily increases the measured phase-space dispersion of the subhalo core. Since the phase-space dispersion is used as a normalising term when determining whether two subhaloes overlap, and hence whether one of the pair will be forcefully disrupted, using larger values makes the condition trigger more frequently.

We recommend not increasing the value beyond the chosen default of $N^{\rm min}_{\rm core} = 20$, as the measured phase-space dispersion will no longer be representative of the subhalo core if its value is comparable to the number of bound particles a subhalo has. In such a case, many premature mergers between well-resolved subhaloes could happen, even if they are physically far away from each other and not comoving with respect to each other. The chosen default therefore represents a strict condition for merging between subhaloes with masses well above the threshold to be self-bound.

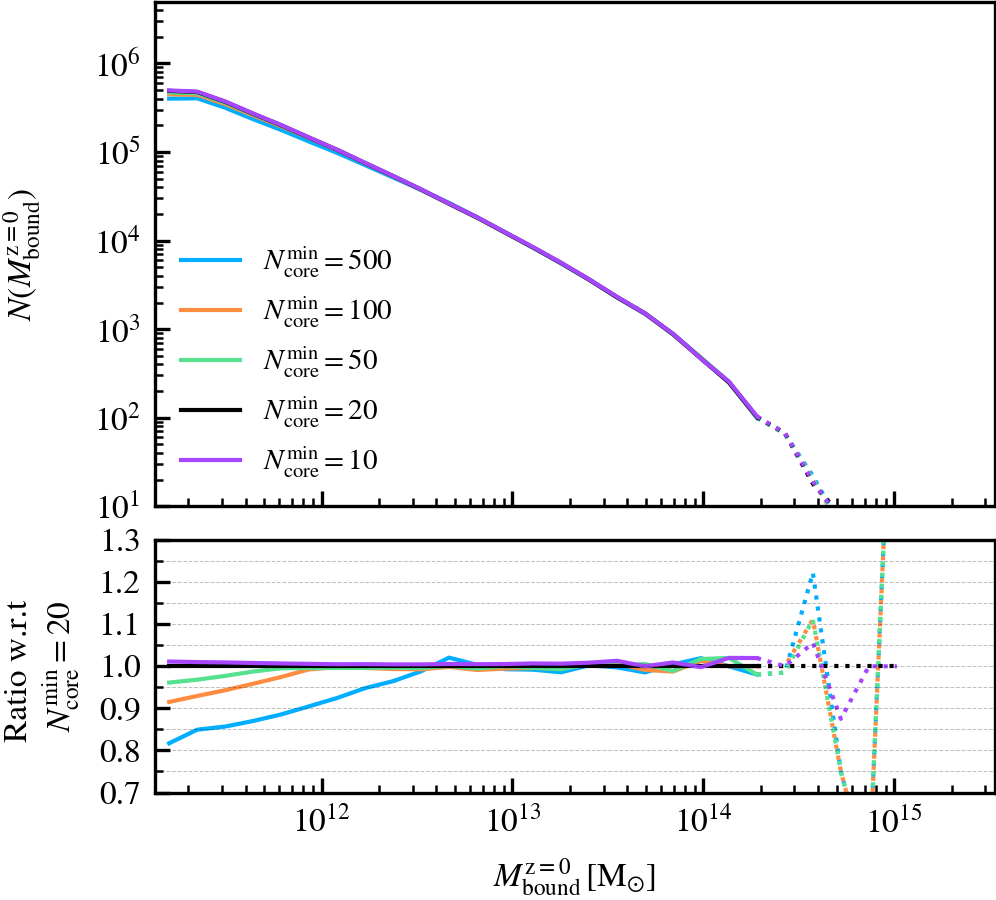
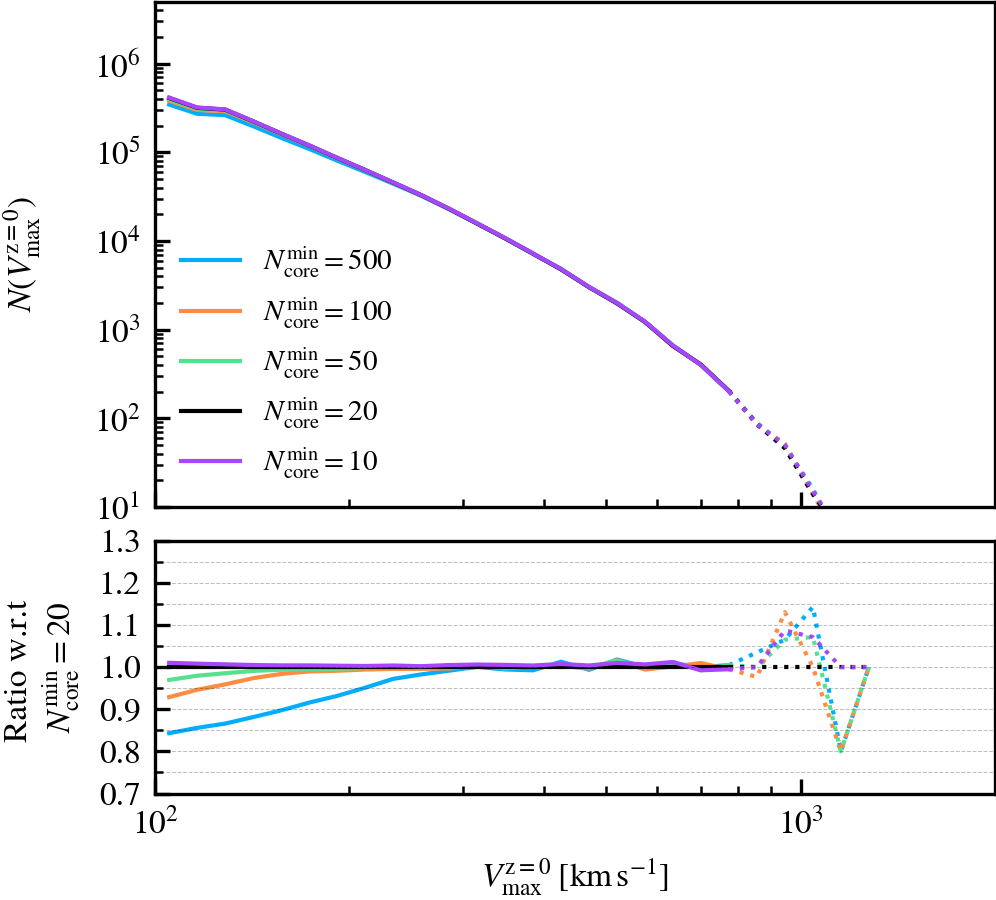
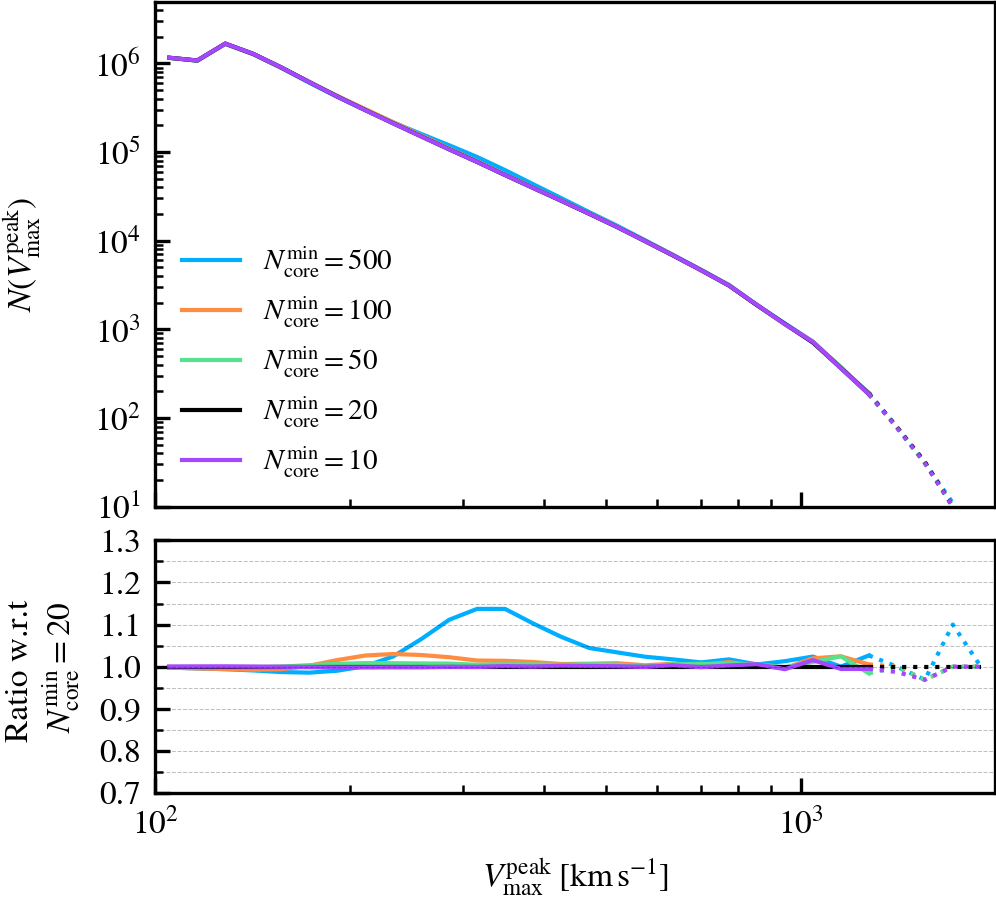
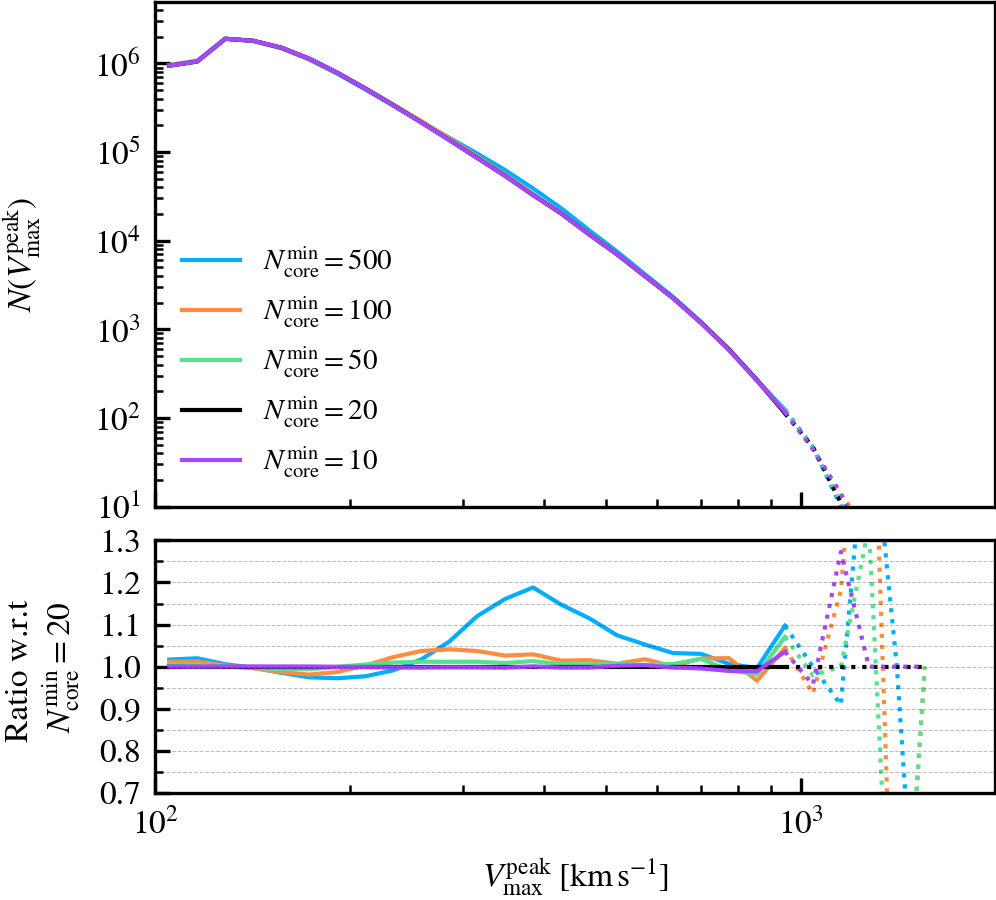
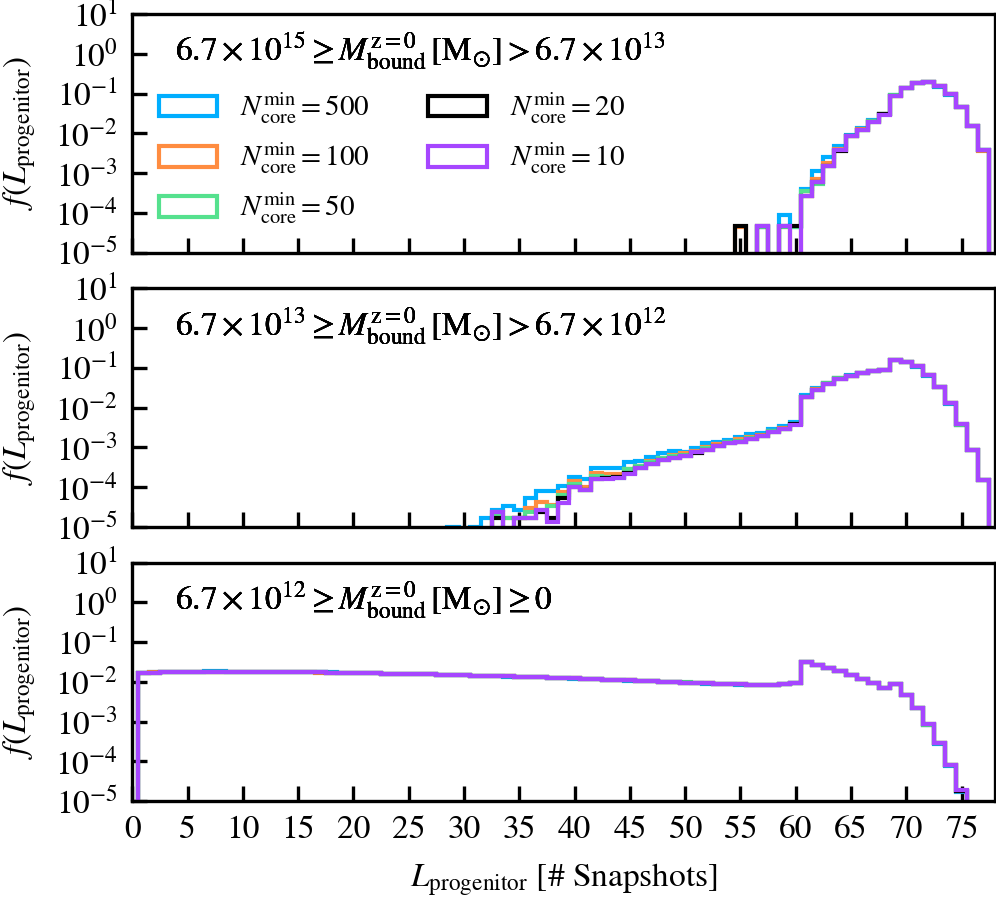
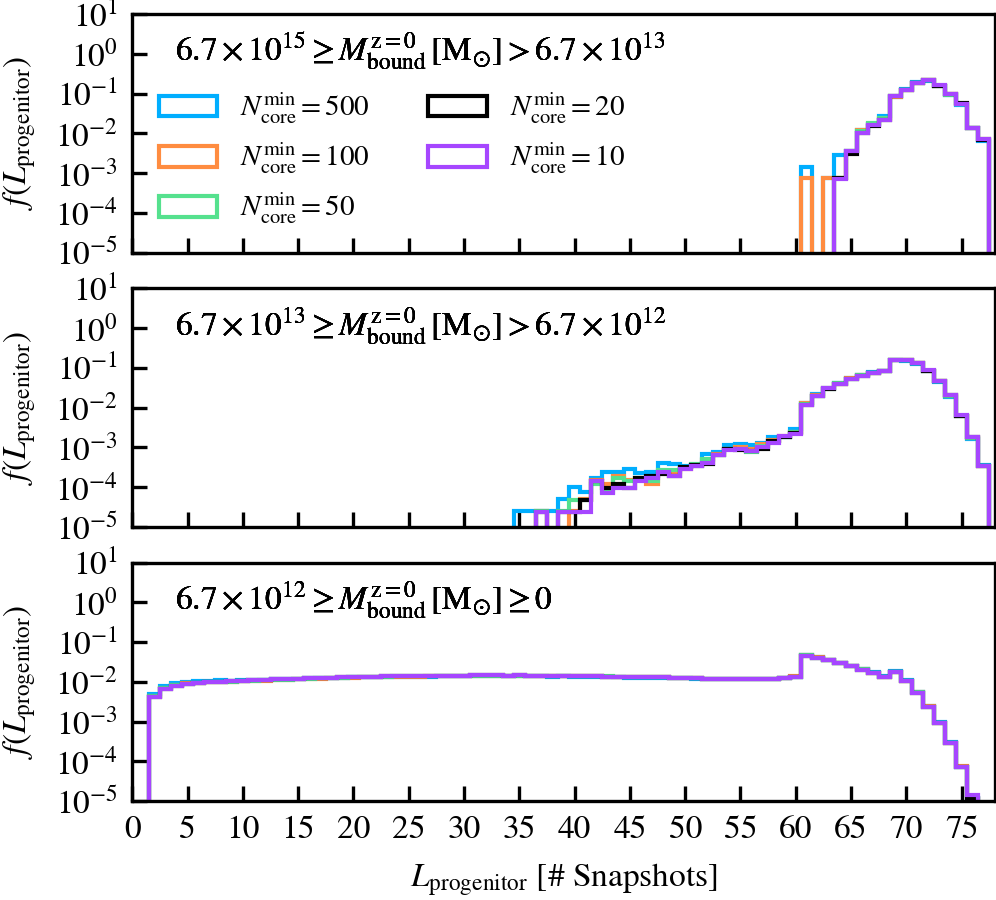
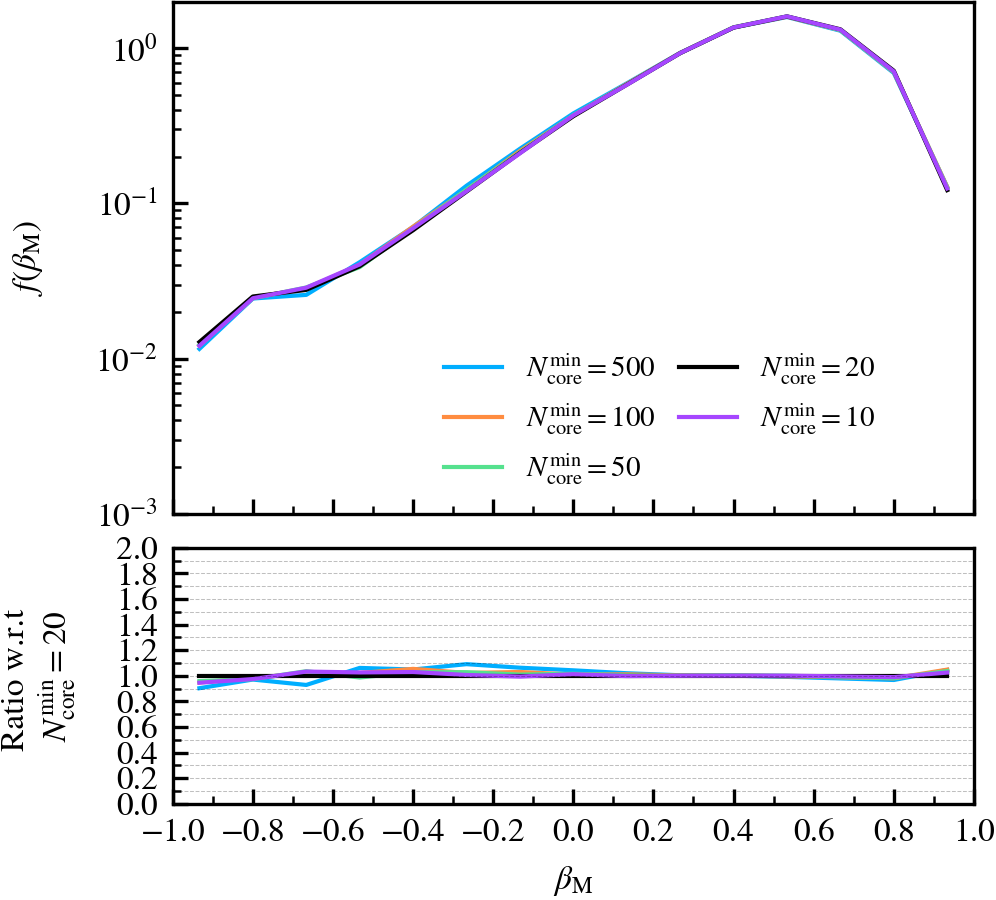
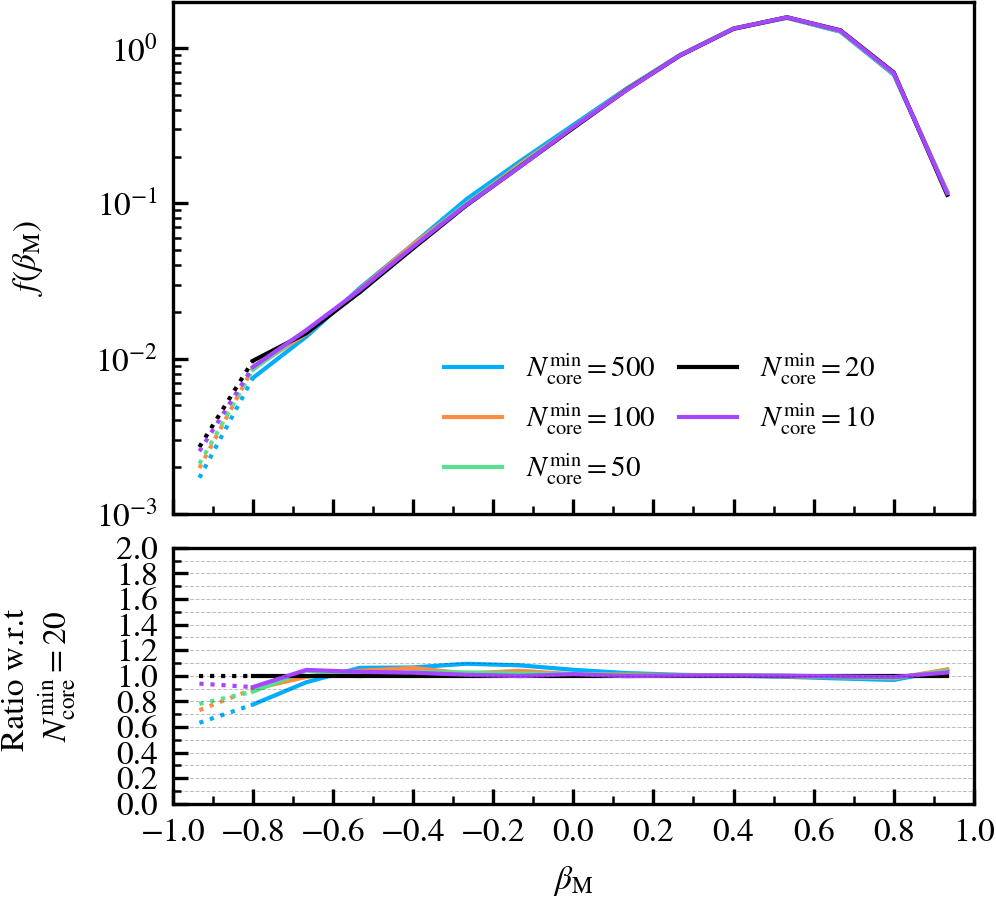
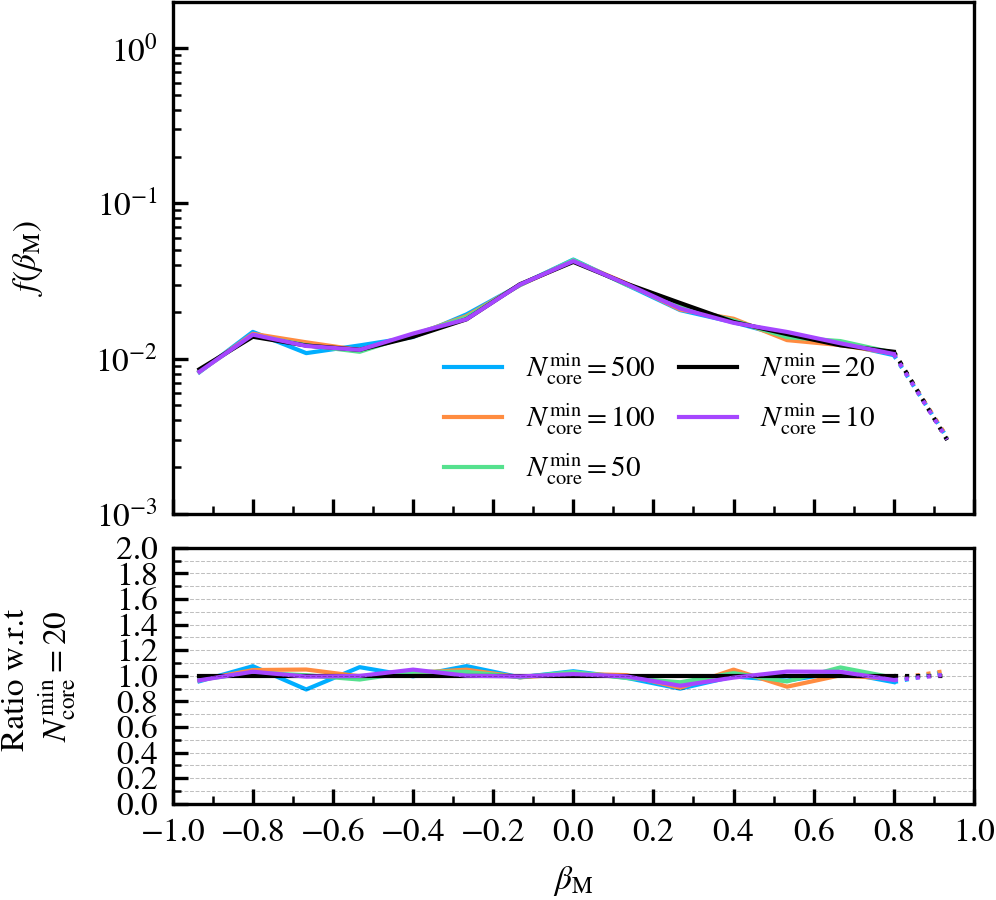
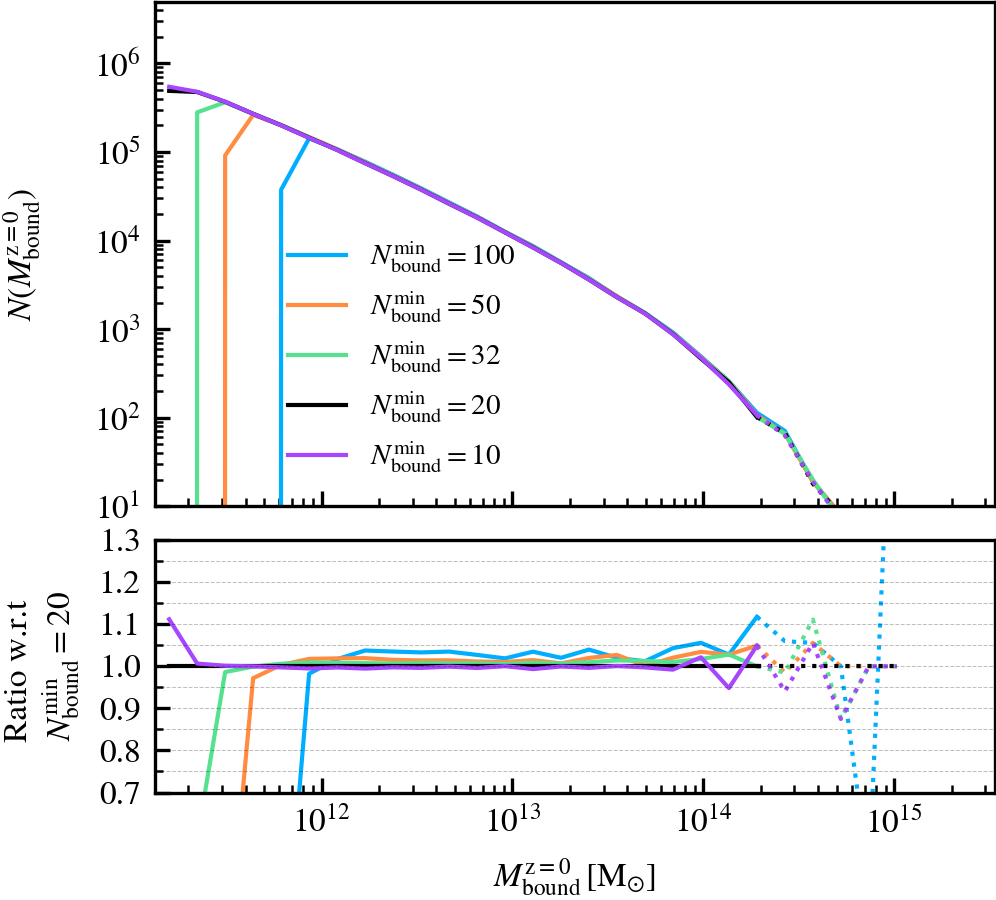
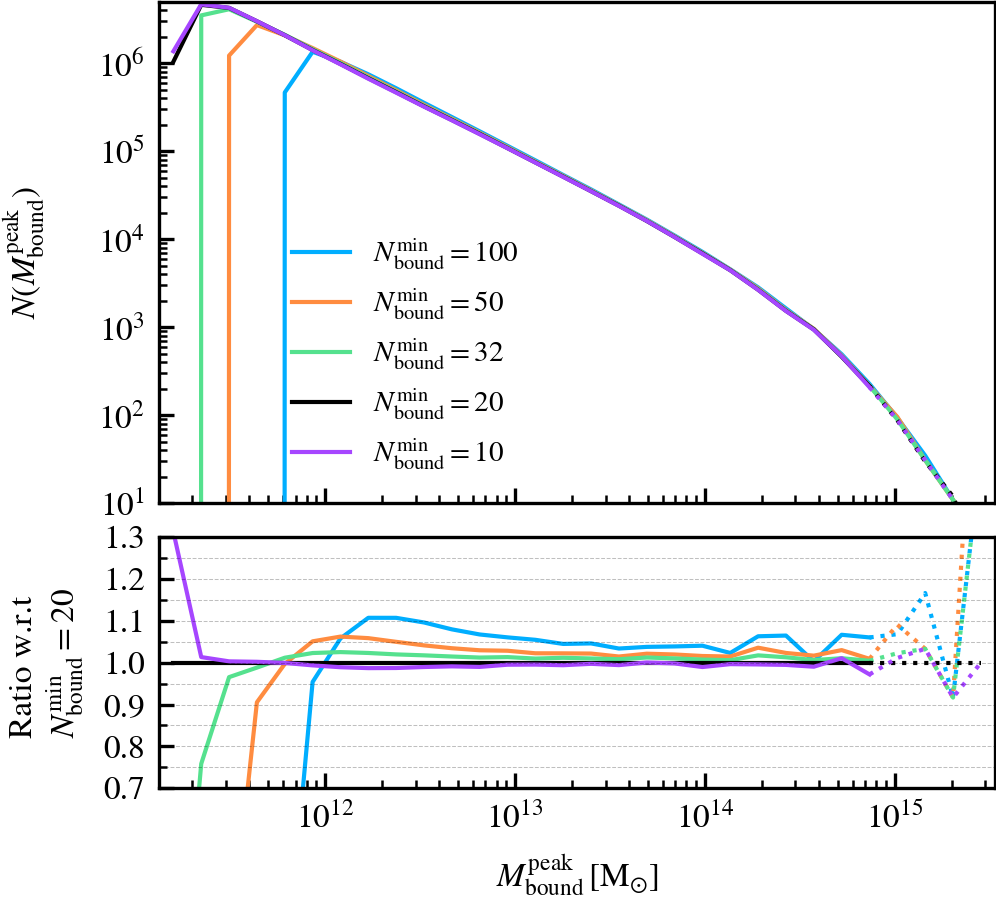
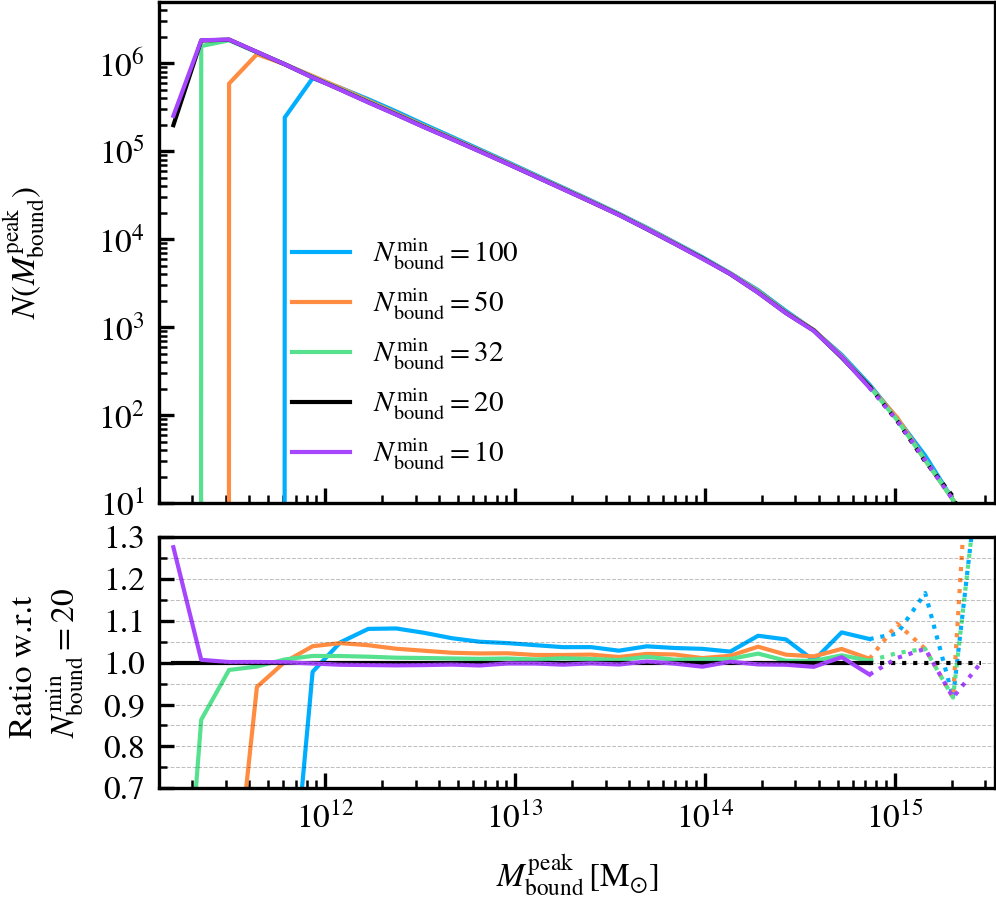
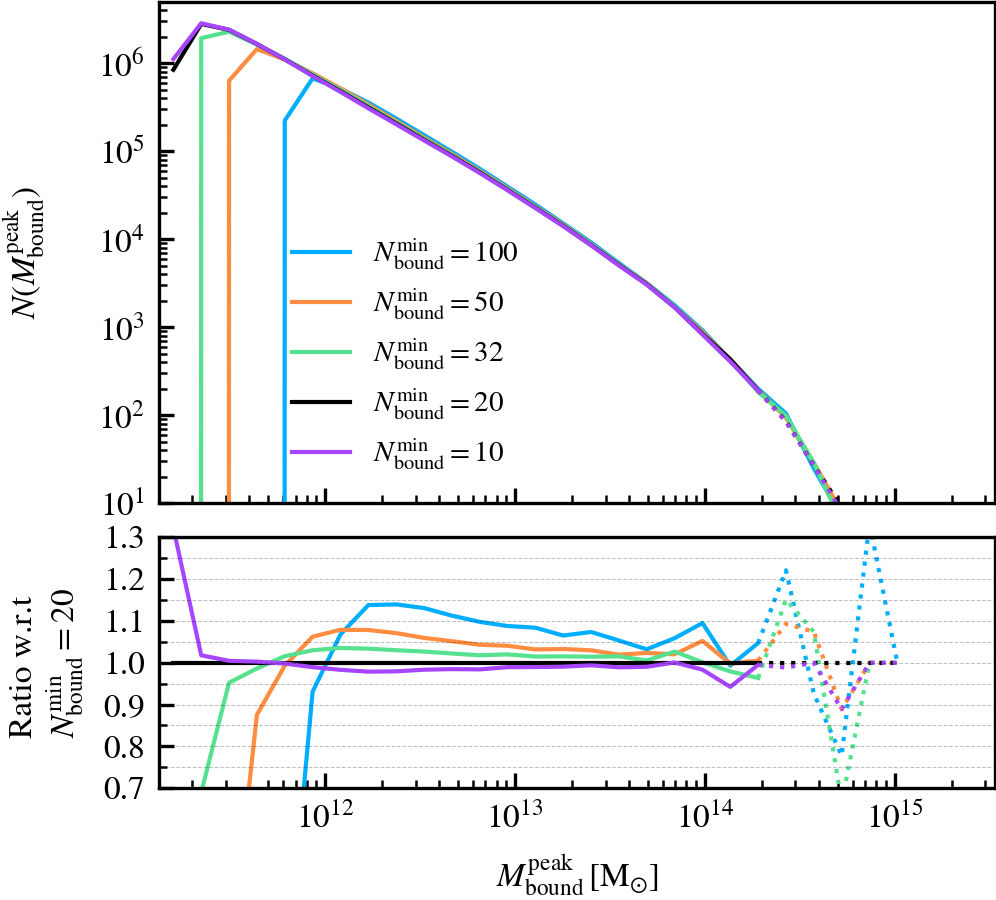
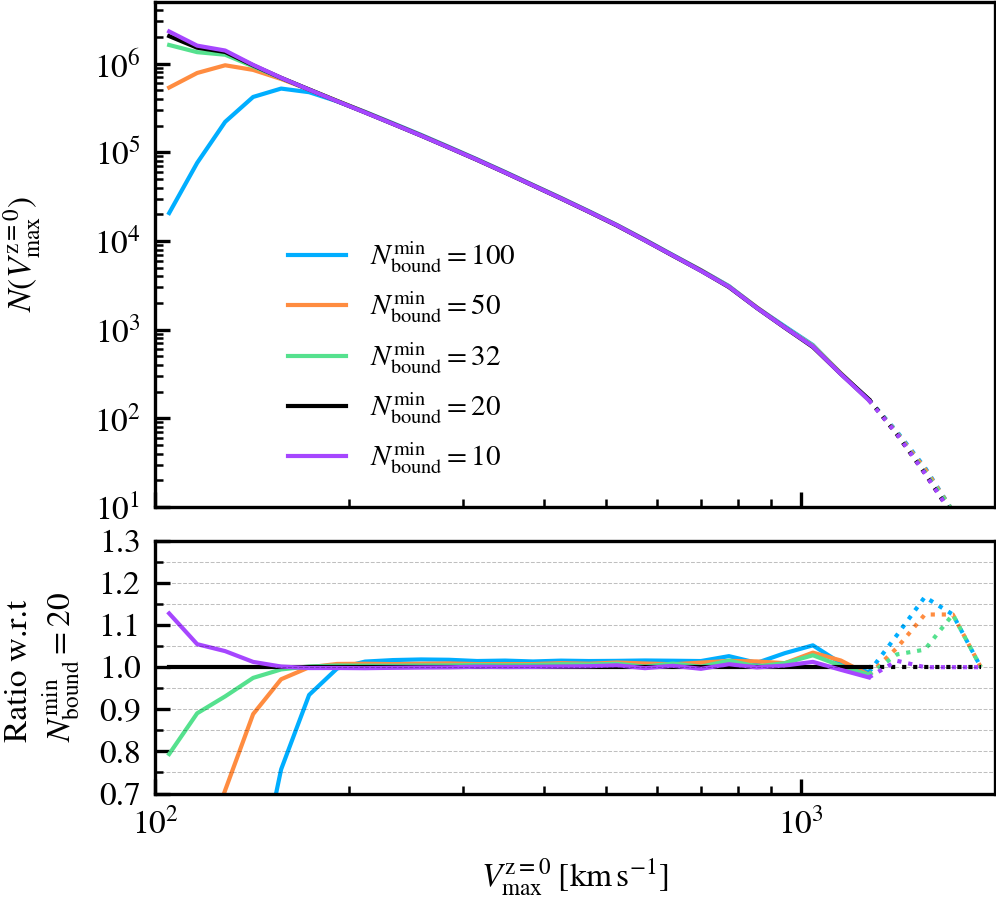
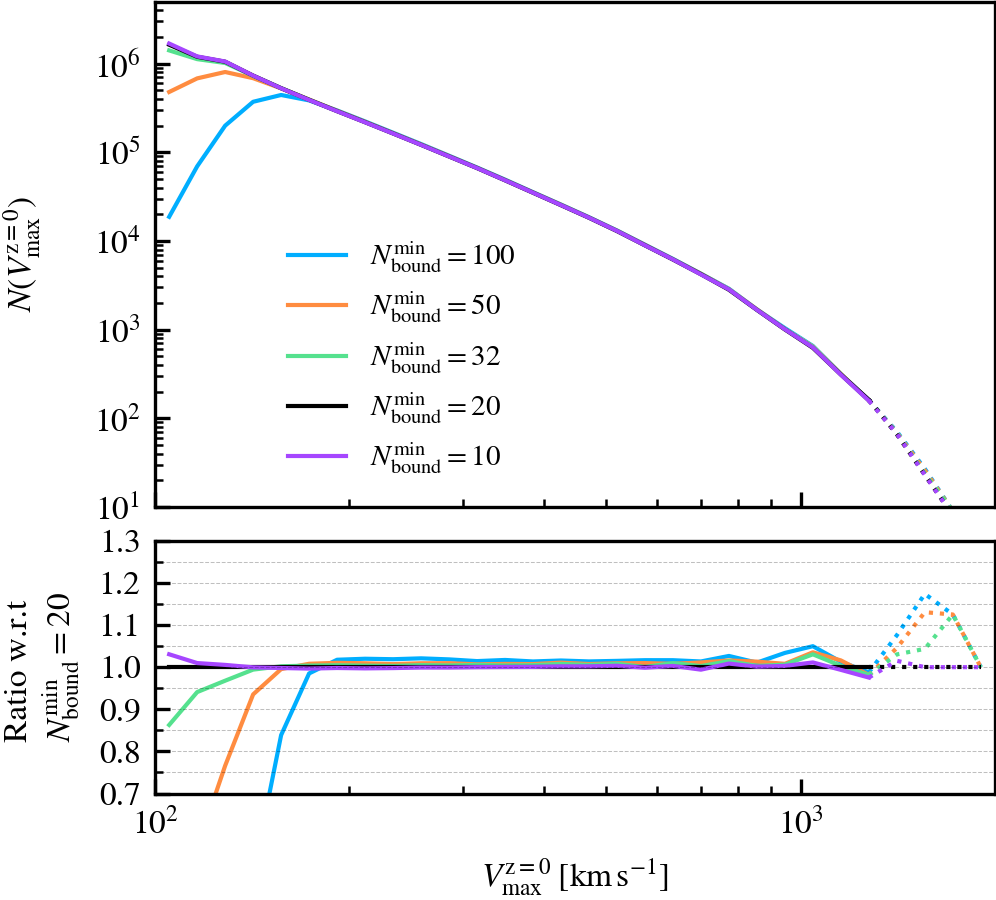
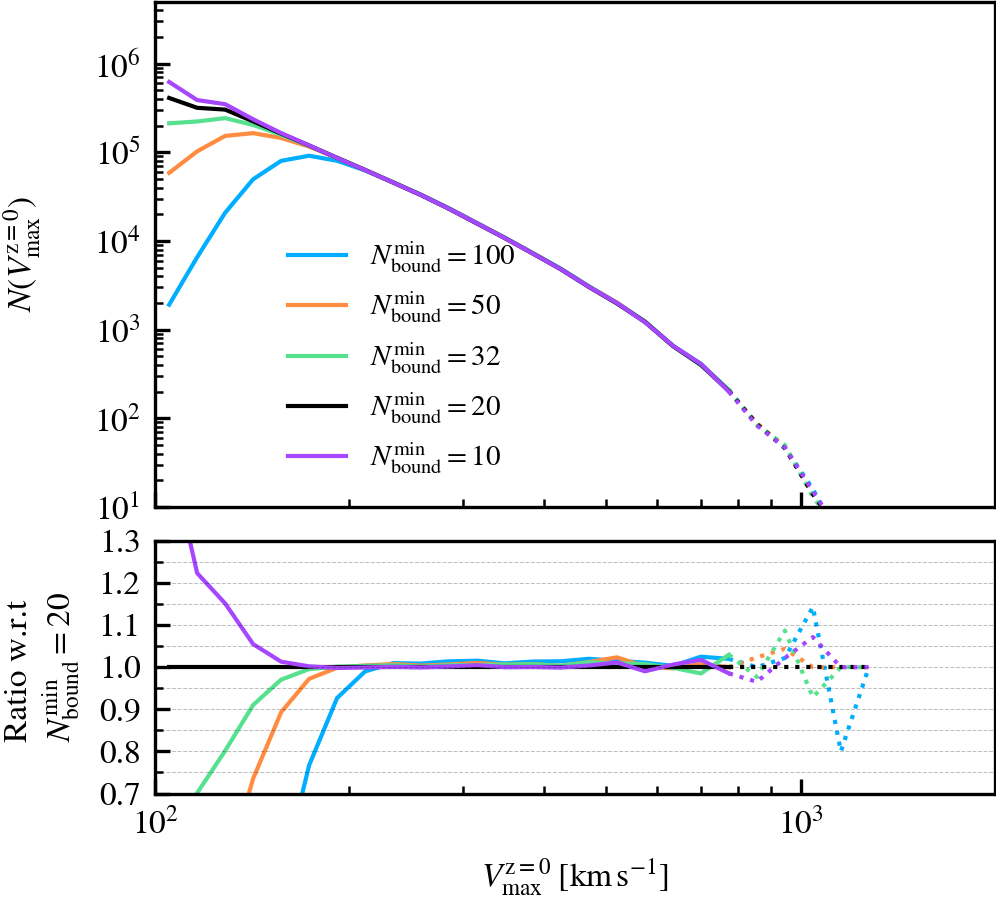
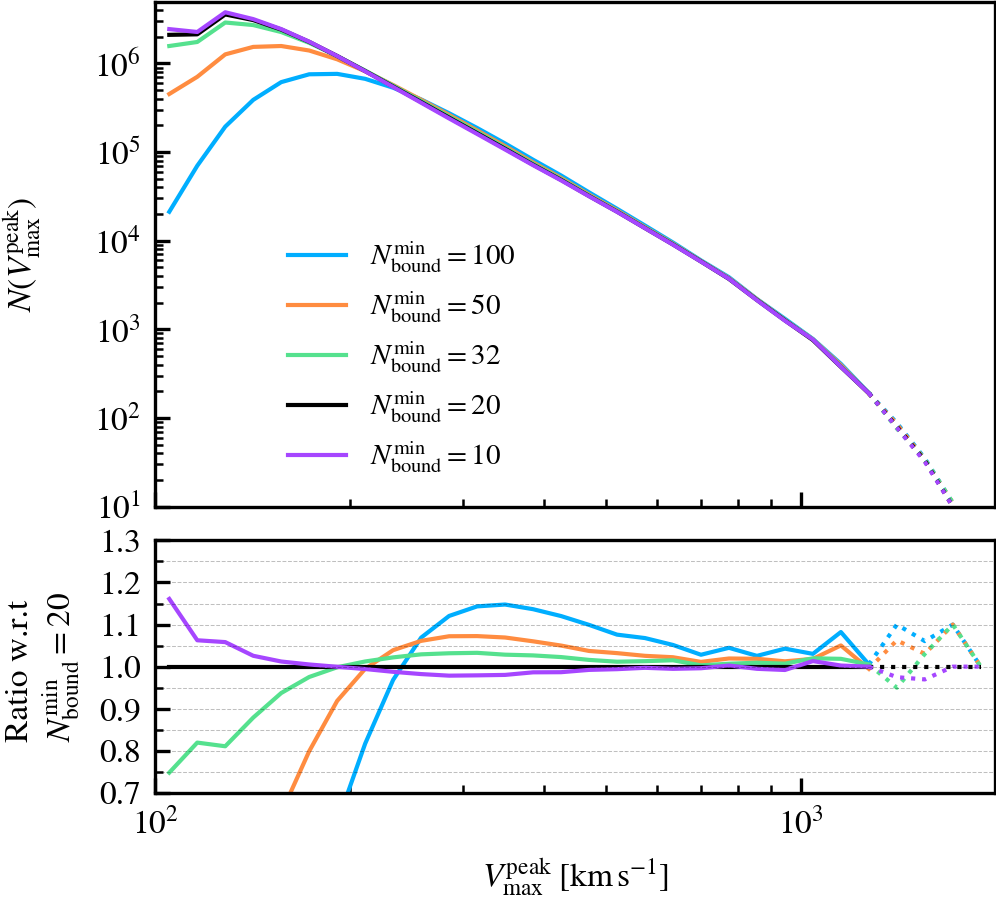
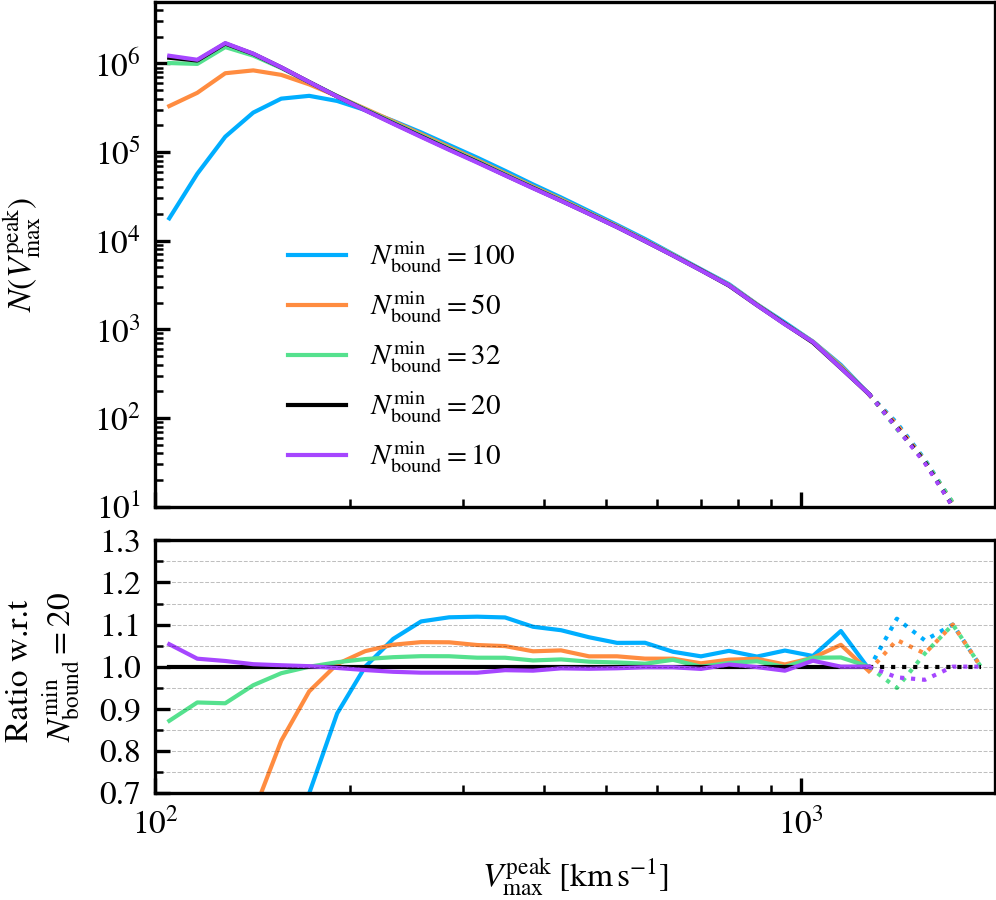
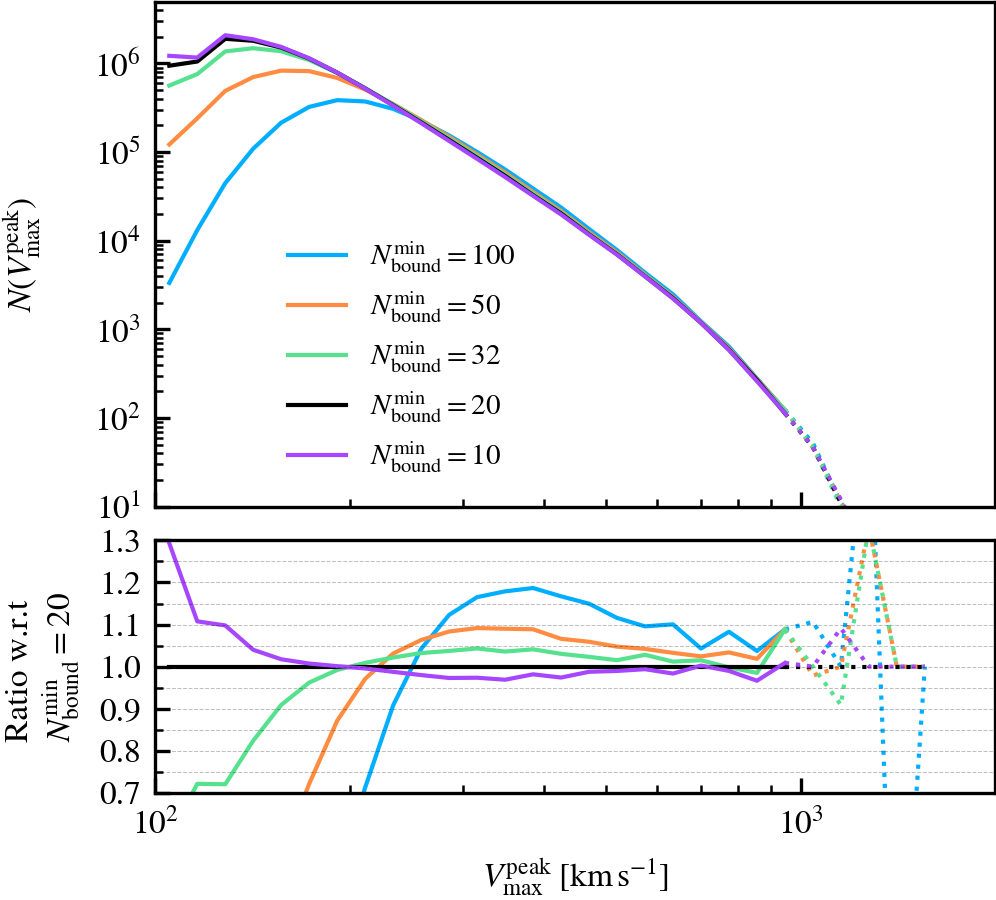
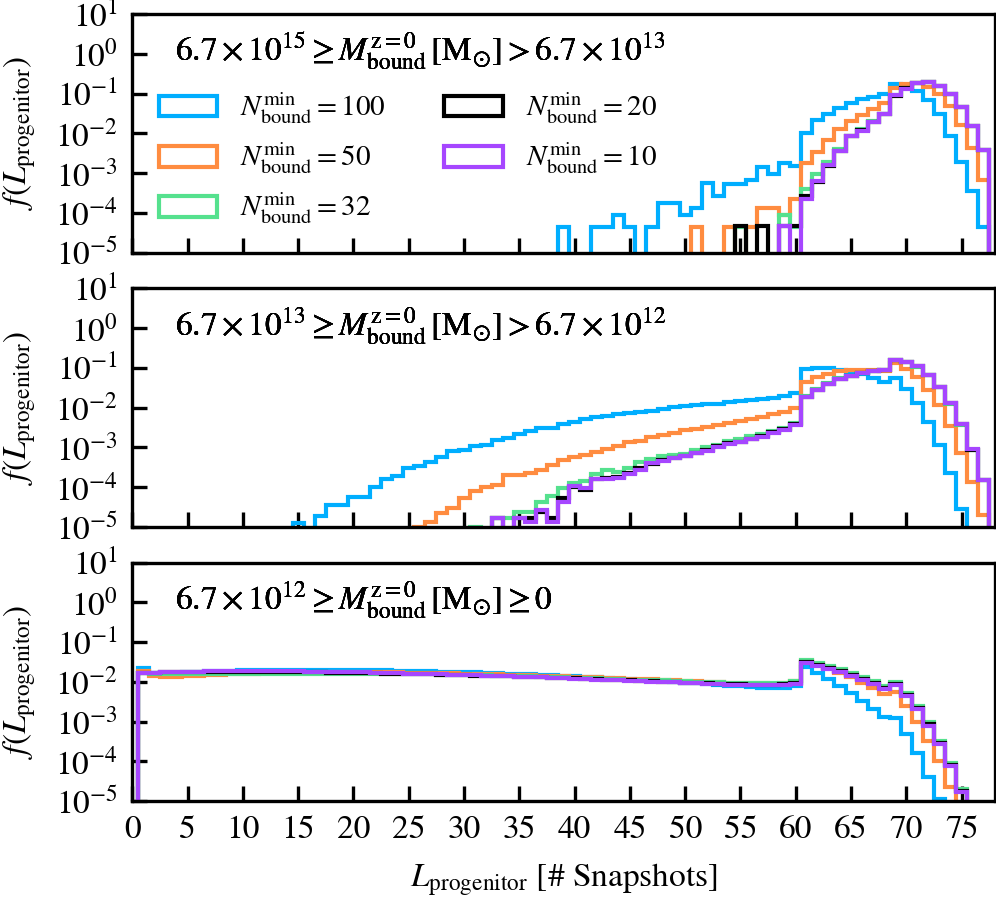
`MinNumPartOfSub`

This parameter, which defaults to $N^{\rm min}_{\rm bound} = 20$, is the minimum number of particles of any type that should be bound to a subhalo for it to be deemed as self-bound. Modifying the value changes the number of subhaloes that are classified as self-bound in the catalogue. This has important implications on the bound mass and velocity functions owing to the fact that HBT-HERONS uses an exclusive mass definition.

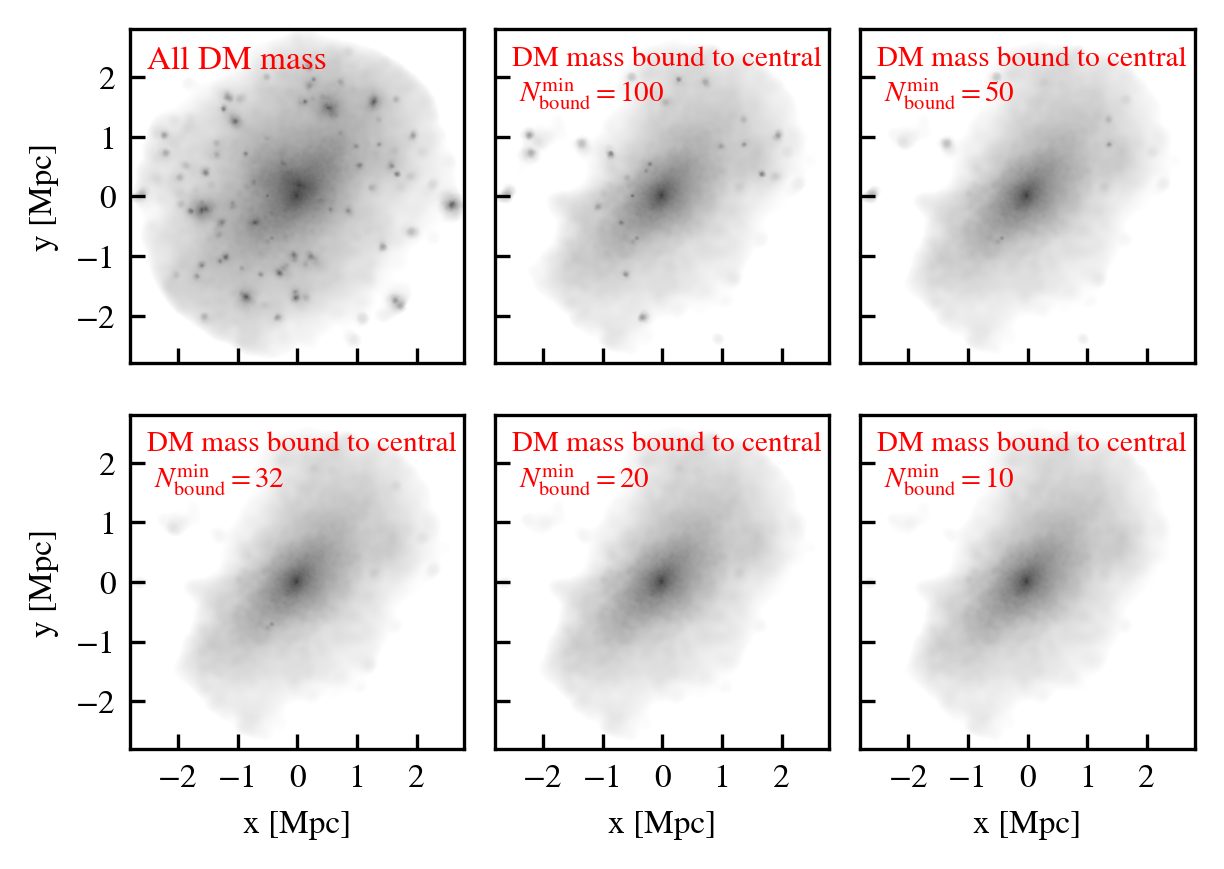
We recommend using a small value of $N^{\rm min}_{\rm bound}$, as "physical" self-bound subhaloes are clearly seen to exist at that cutoff scale. Indeed, we see in the supplementary plot that virtually all residual clumps of self-bound dark matter are removed from the set of particles bound to the central when using $N^{\rm min}_{\rm bound} \leq 20$. We advise against lowering the value below 20, since the computational and data storage requirements increase drastically due to the fact that low mass subhaloes are much greater in number than massive subhaloes. It additionally increases the chances of spurious subhaloes to be detected as self-bound.

Supplementary plot

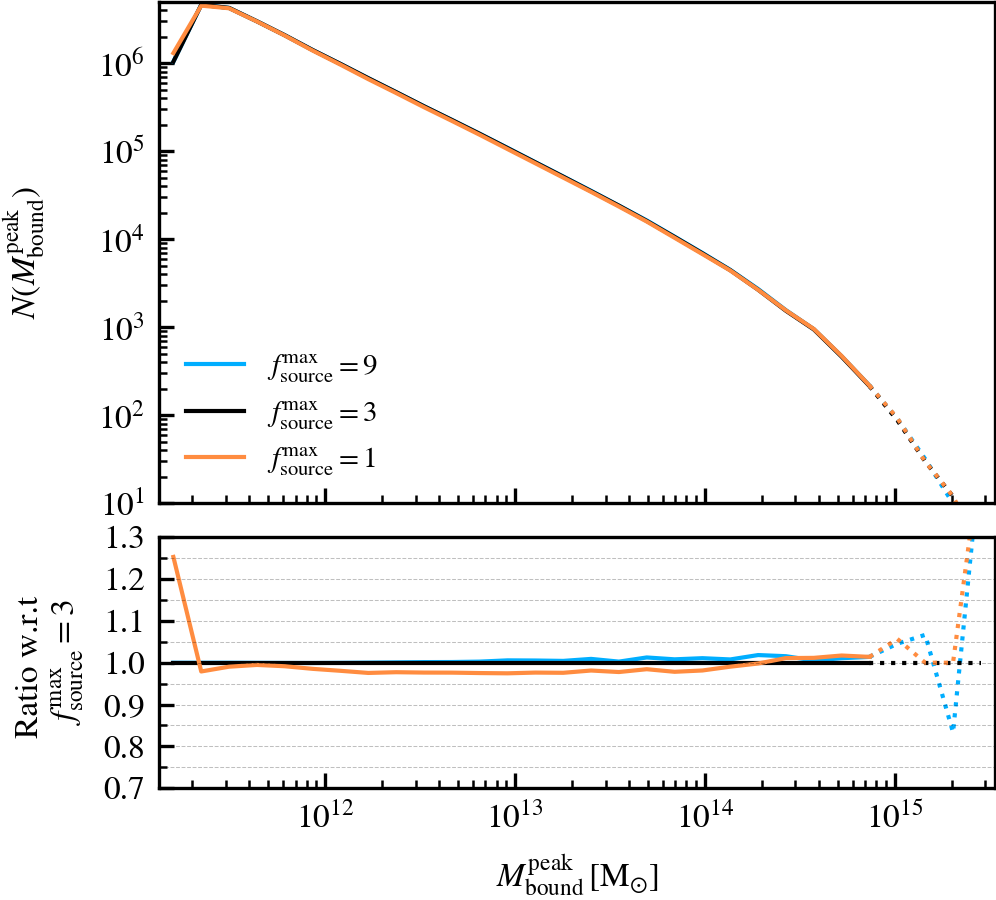
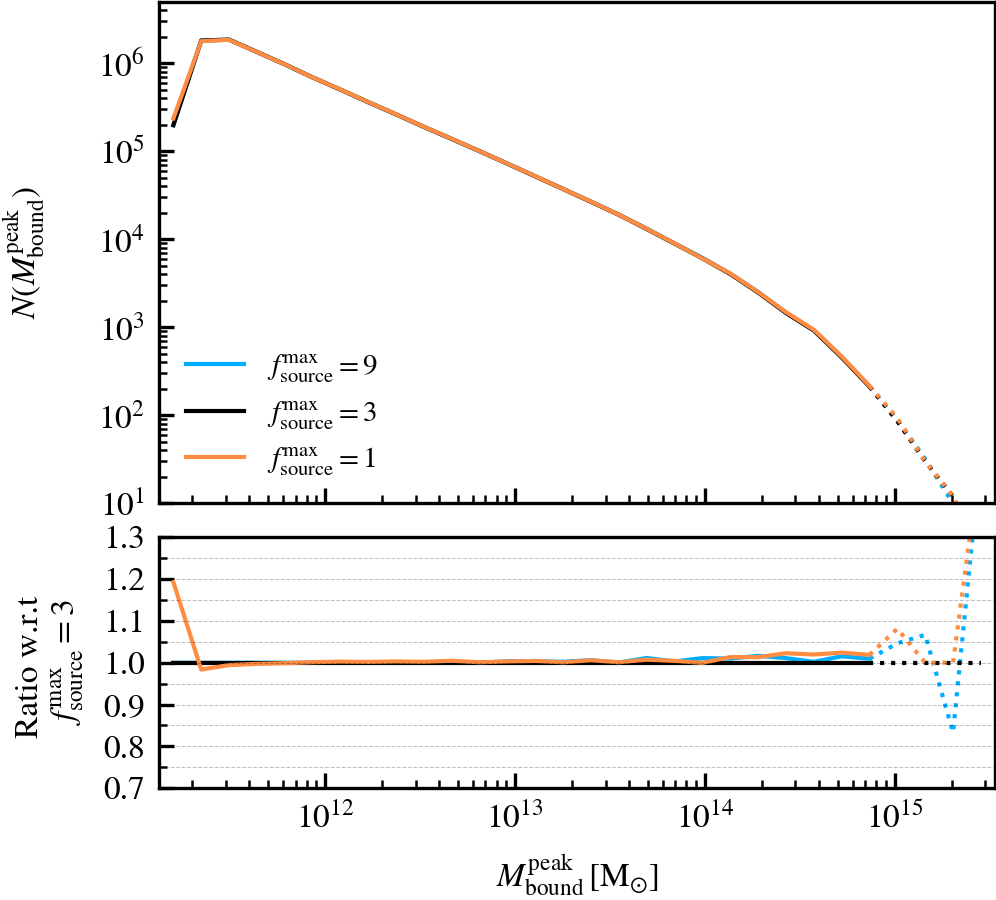
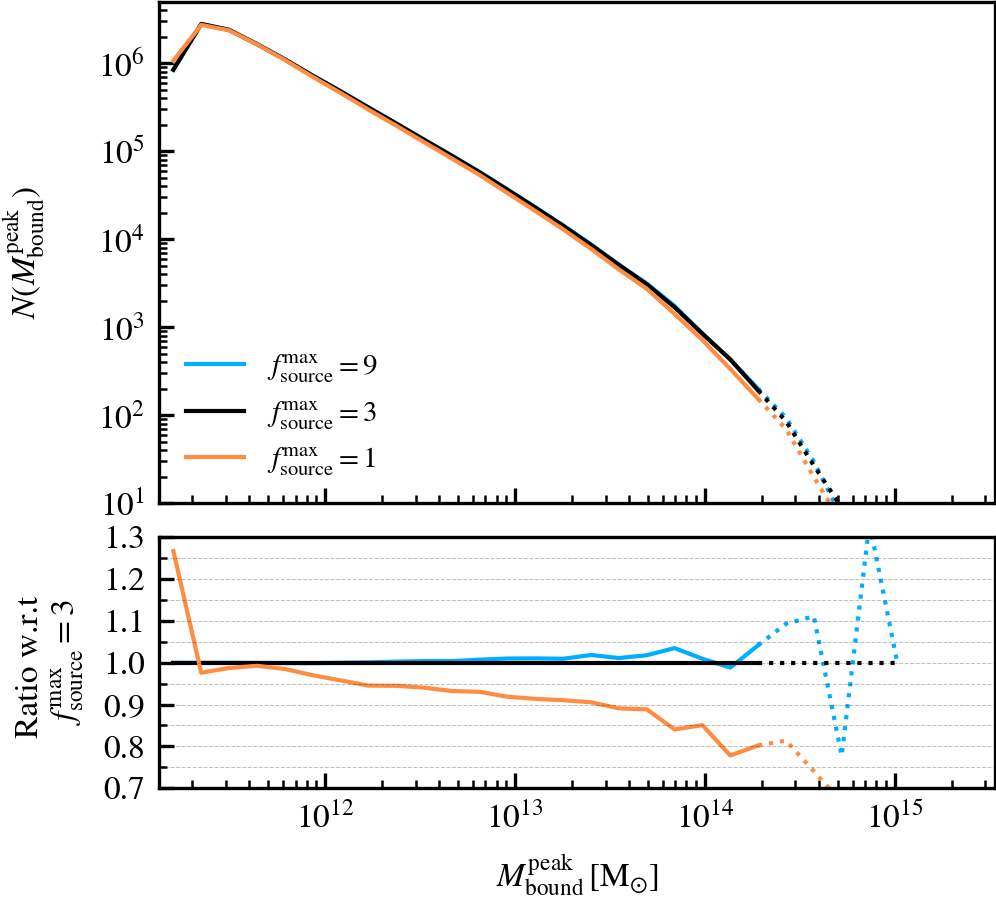
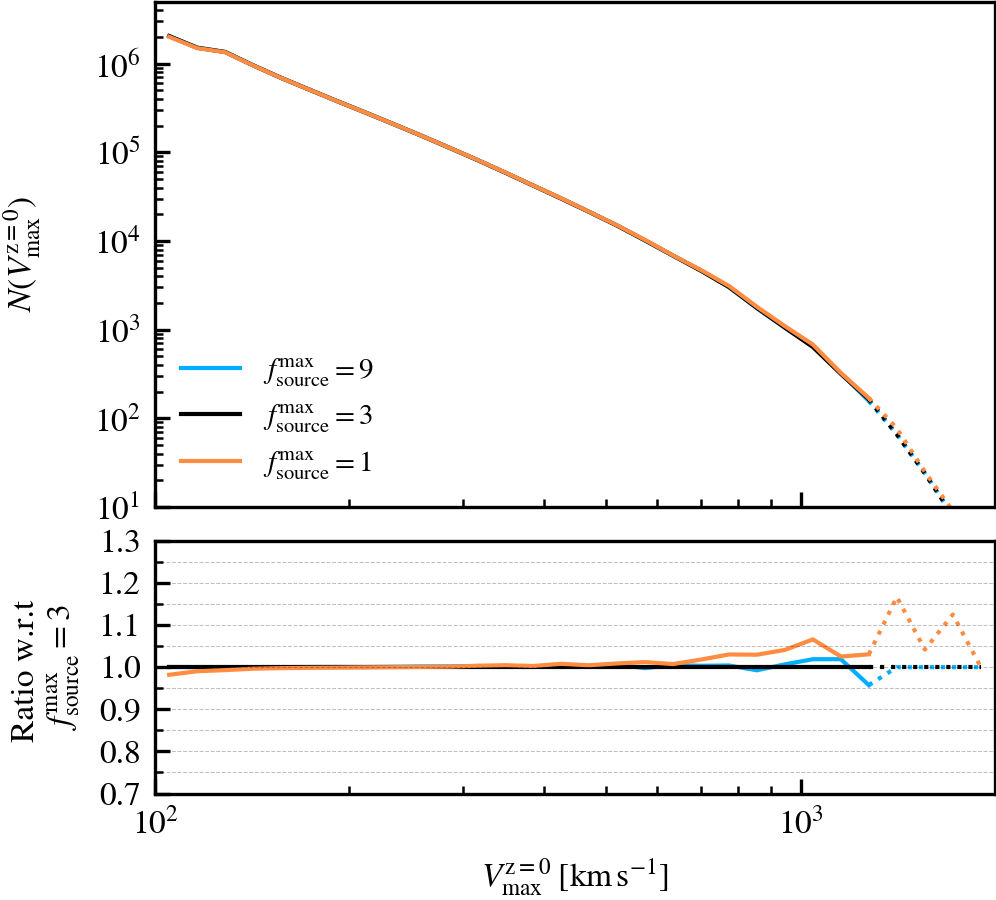
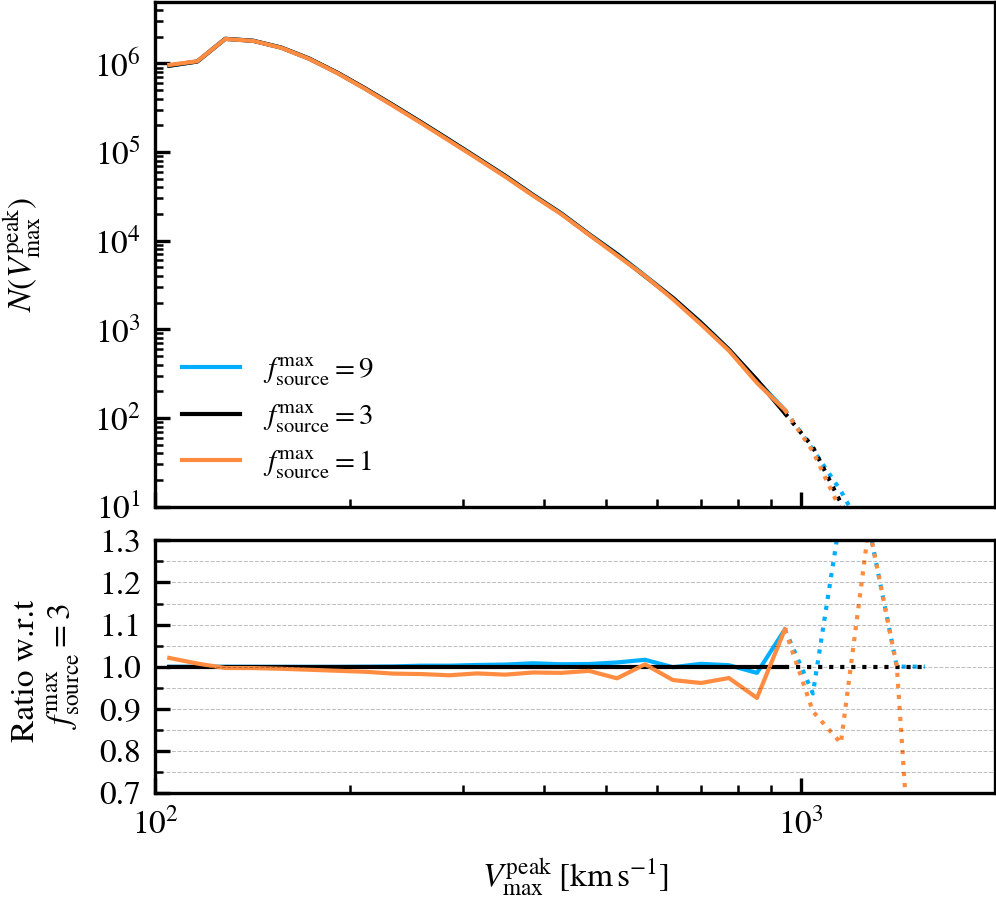
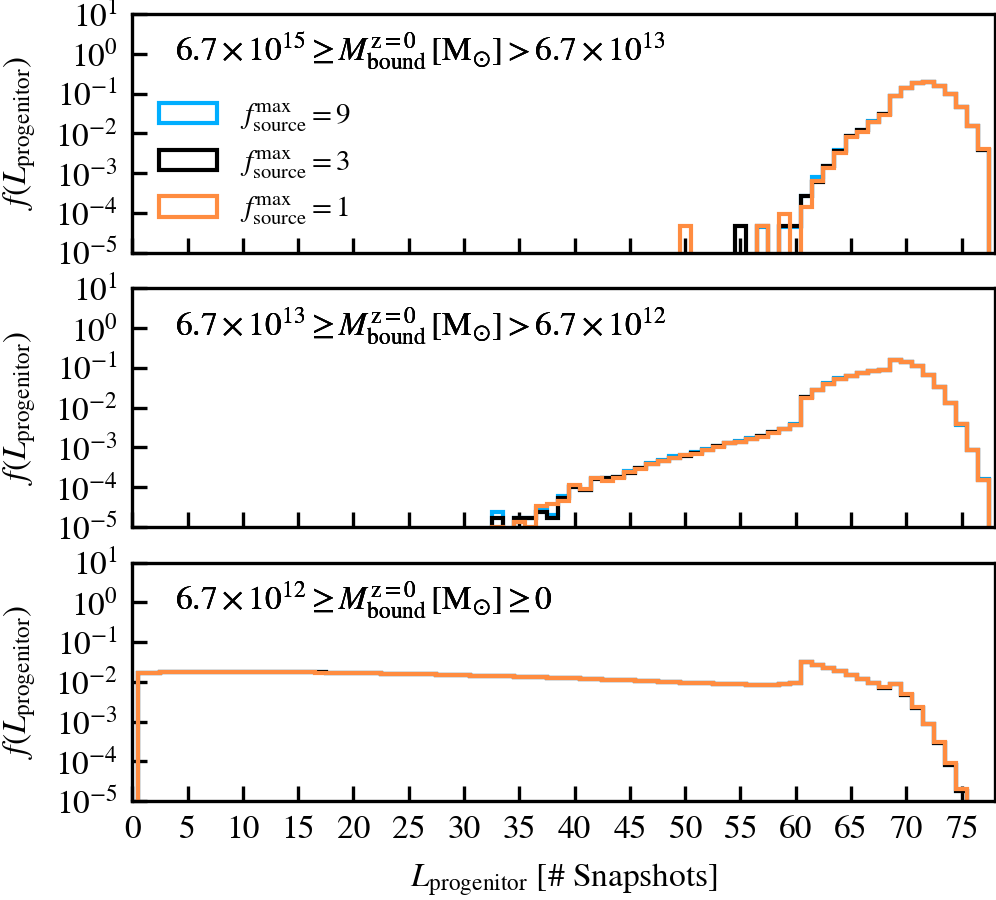
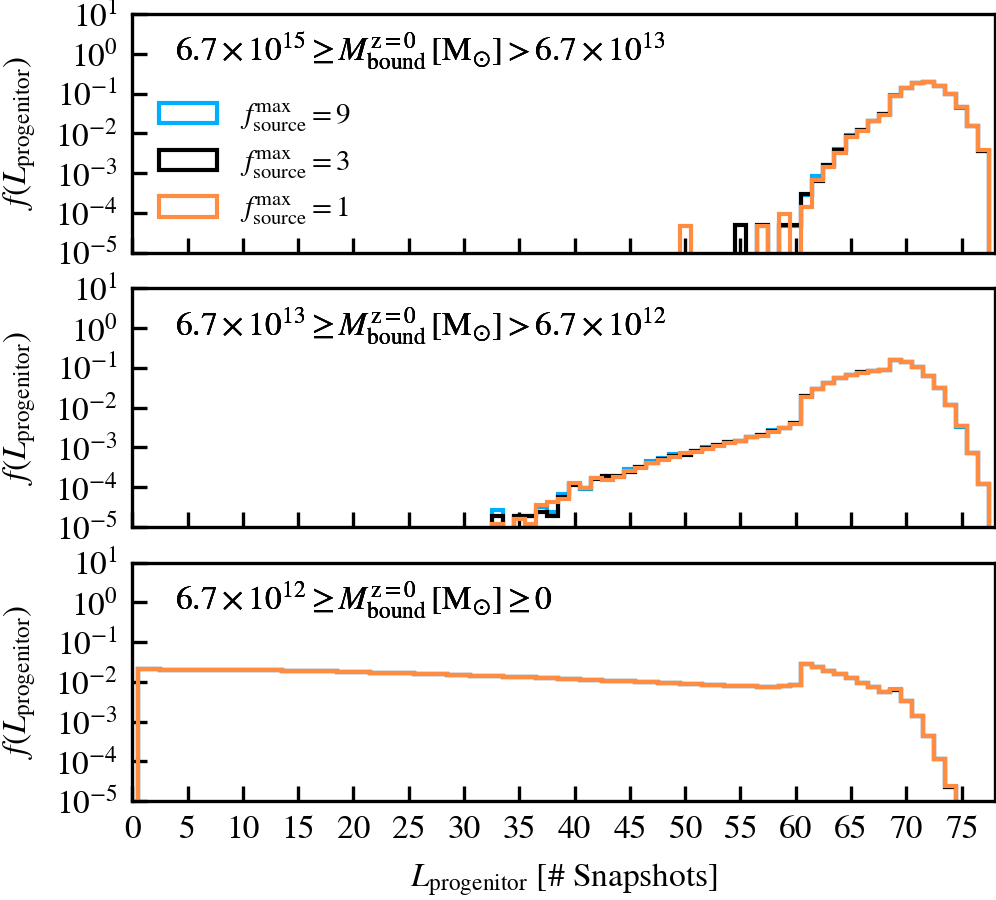
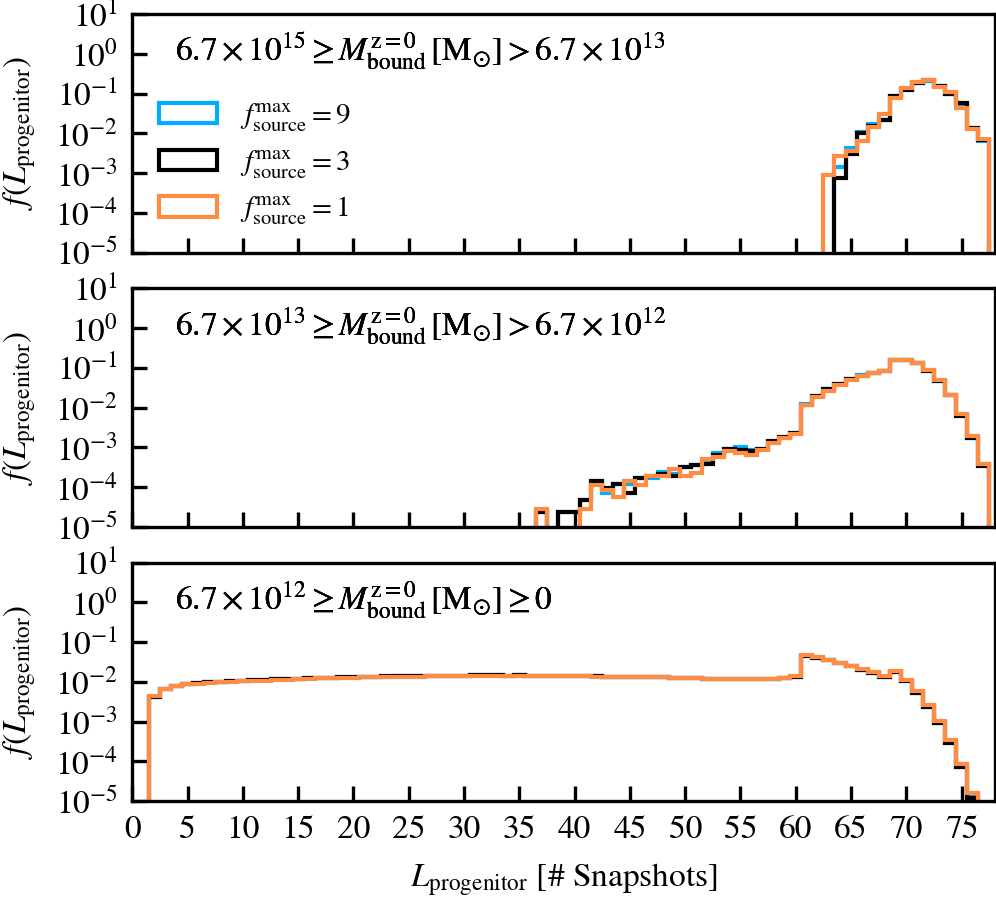
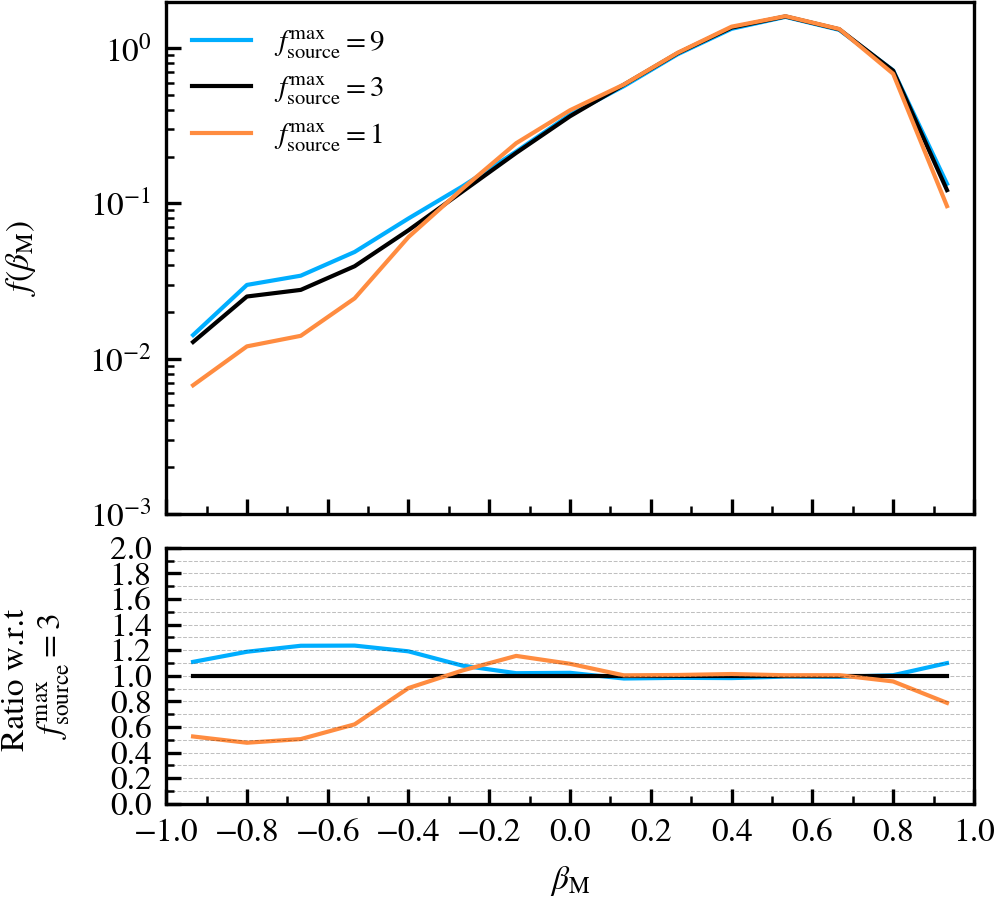
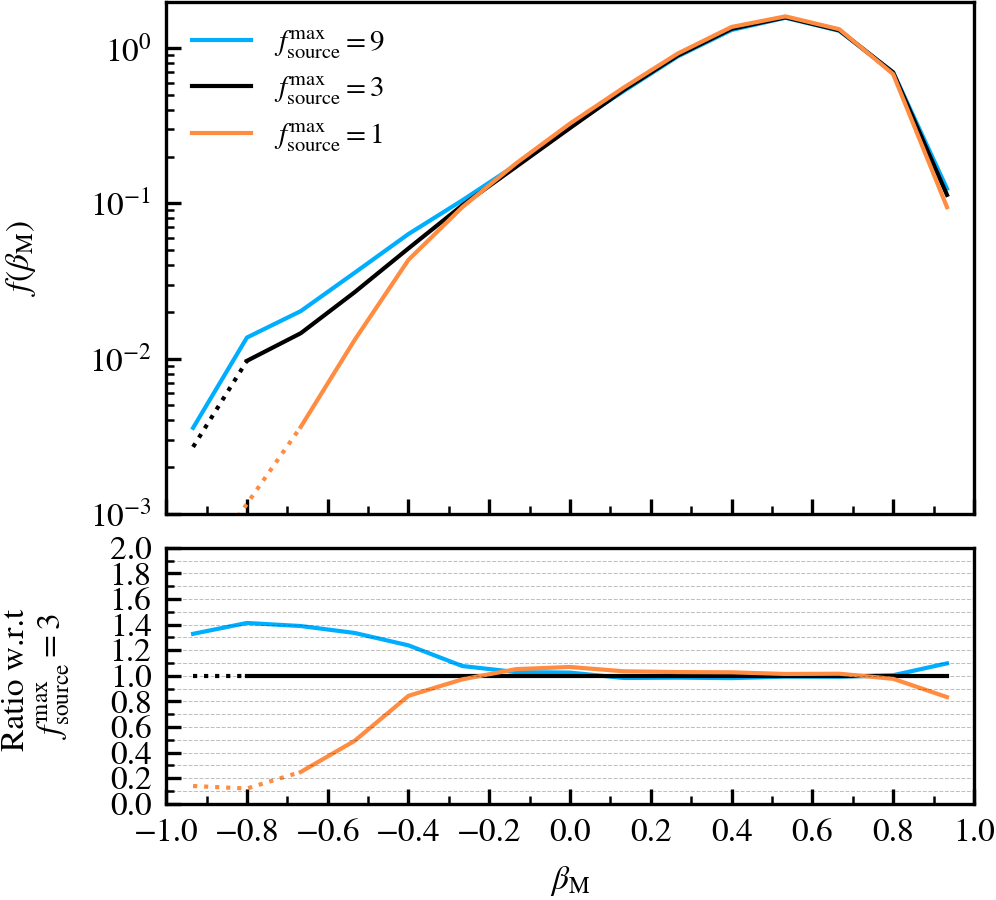
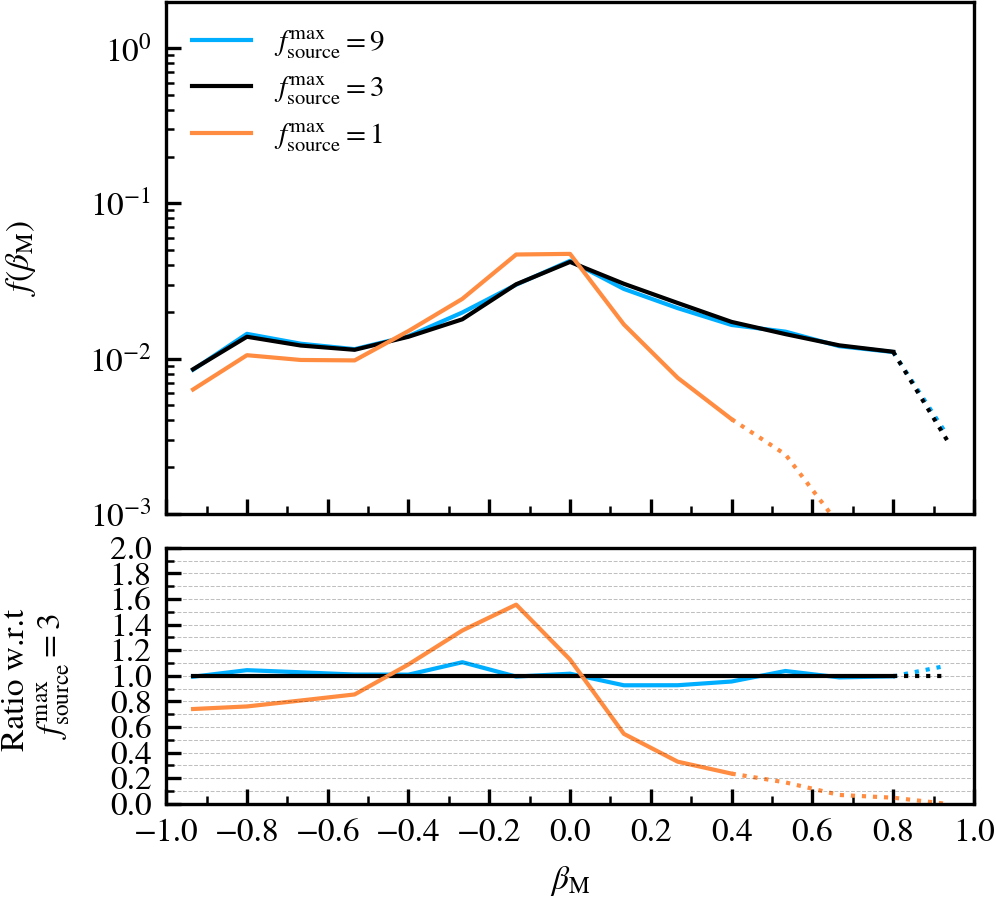
`SourceSubRelaxFactor`

This parameter, which defaults to $f^{\rm max}_{\rm source} = 3$, determines how many particles a subhalo can have associated to it relative to the number of bound particles it has. Its primary use is to allow particles that were previously bound to a satellite subhalo to be "re-accreted". This can for example happen after a pericentric passage, where the tidal forces may make some amount of mass unbound, which may later found as bound once the tidal perturbations have subsided. This can also happen secularly, since any given particle may be unbound in a single output by pure chance.

We recommend using a value that is larger than $f^{\rm max}_{\rm source} = 1$, to prevent the secular loss of mass over time. Any particle that is momentarily unbound will lose its association the subhalo it belonged to, preventing its reaccretion at a later time. Over time, this leads to the secular decrease of mass of satellites, which stunts their mass growth. Despite the fact that larger values than the default do not affect results based on our tests, we advise using much larger values than the default. First, the computational cost increases. Second, the retention of too many unbound particles in the source can affect the centre of mass estimate of a subhalo. As its position and velocity plays an important role during unbinding, it can lead to premature, artificially-induced disruption.